Coordinate systems are an integral part of your Electromagnetic study. While solving EMT problems, we often need to convert between coordinate systems. And, while obtaining PHI coordinates either for Cylindrical or Spherical from the Cartesian coordinates, many students do this mistake. Let’s see how to avoid it.
Need of Coordinate system in Electromagnetics
In electromagnetics, a coordinate system is a crucial tool used to describe the position and motion of electromagnetic fields in space. It is used to define the location, direction, and magnitude of electric and magnetic fields and to analyze and predict the behavior of electromagnetic waves. You cannot imagine EMT without Coordinate system.
There are several reasons why a coordinate system is necessary in electromagnetics:
- To describe the position and motion of charged particles either electric charge or magnetic monopole/dipole.
- To define the location, direction, and magnitude of electric and magnetic field.
- To analyze and predict the behavior of electromagnetic waves.
- To understand Antenna propagation.
- Transmission lines.
Transformation between Coordinate Systems
In electromagnetics, it is common to work with different coordinate systems, such as Cartesian, cylindrical, and spherical coordinates.
We select Coordinate system based on the need of the problem we are solving.
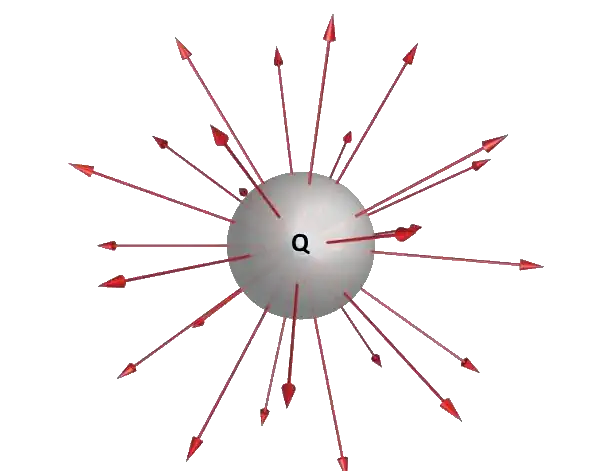
For such kind of geometry we would go with Spherical Coordinate System.
While for such type of geometry, Culindrical Coordinate system would be the best fit.
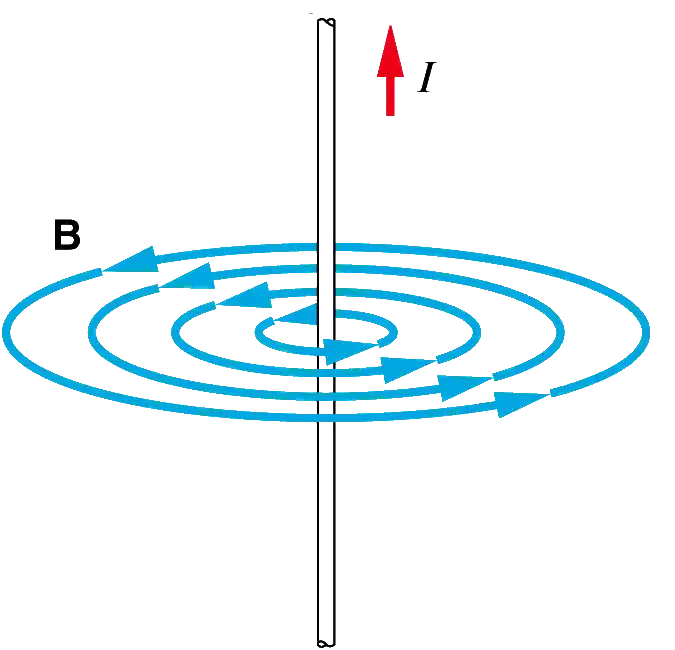
So many times we need to transform between the coordinate systems according to the need.
Conversion between Cylindrical and Cartesian Coordinate Systems
In cylindrical coordinates, the coordinates are usually denoted as (ρ, φ, z), while in Cartesian coordinates, they are denoted as (x, y, z).

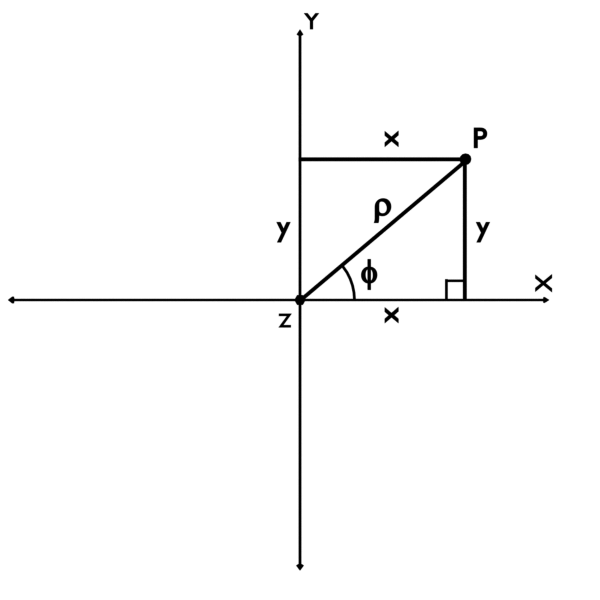
The transformation from the cylindrical coordinates (ρ, φ, z) to the Cartesian coordinates (x, y, z) as follows:
x = ρ cos(φ)
y = ρ sin(φ)
z = z
The transformation from the Cartesian coordinates (x, y, z) to the cylindrical coordinates (ρ, φ, z) as follows:
\rho=\sqrt{(x^2+y^2)} \phi=\tan^{-1}\left(\frac yx\right)z = z
The problem of PHI
The formula \phi=\tan^{-1}\left(\frac yx\right) won’t give you the correct answer always.
For example consider points (1,1,0) and (-1,-1,0). Both are completly different points. One is in the first quadrant while other in the third one.

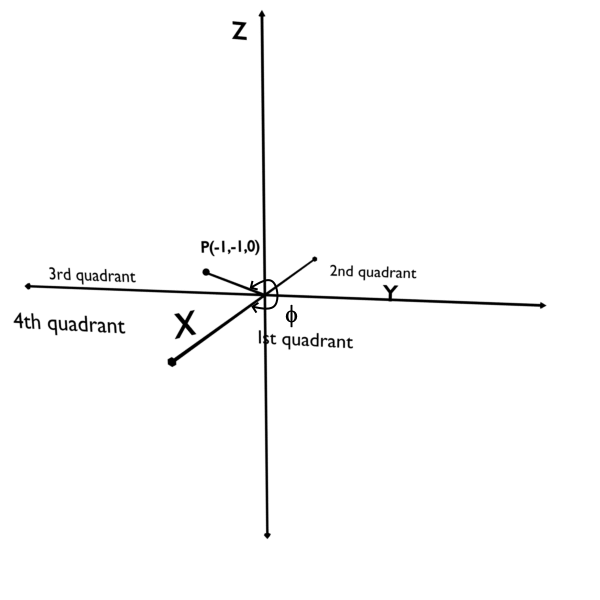
But, your formula \phi=\tan^{-1}\left(\frac yx\right) will give you exactly the same phi for both the points. This is absolutly wrong as you can see from the figures above.
So, always remember, use this formula as shown in the figure below. Put y by x into the mod and based on the quadrant of the point, we need to add or substract certain angle manually.

Case 1: Point is in the First quadrant of XY plane
No need to worry. Your answer given by the formula tan inverse of mod of y by x will give you the correct answer.
Case 2: Point is in the Second quadrant of XY plane
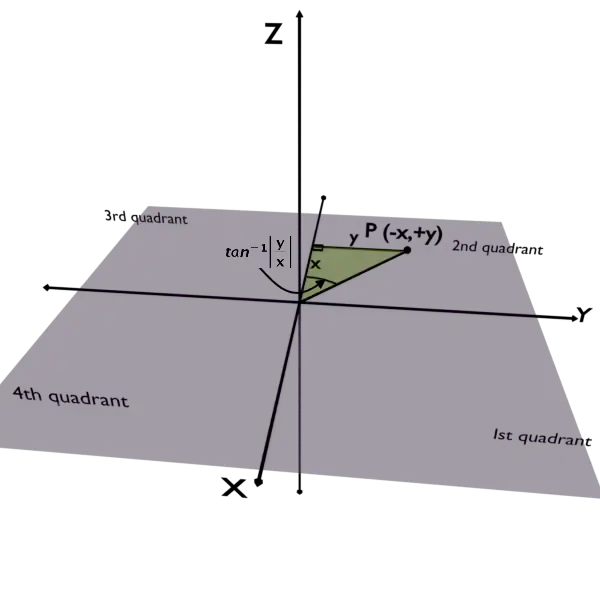
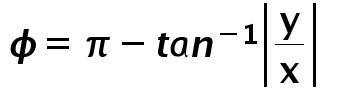
Case 3: Point is in the Third quadrant of XY plane
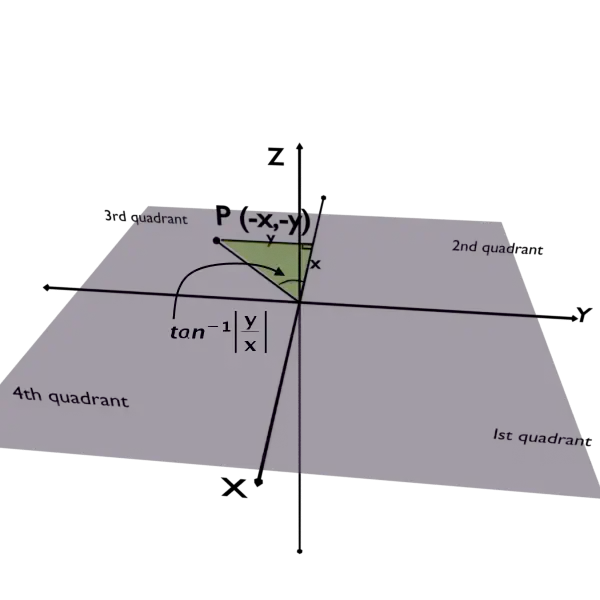
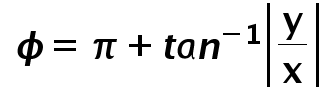
Case 4: Point is in the Fourth quadrant of XY plane
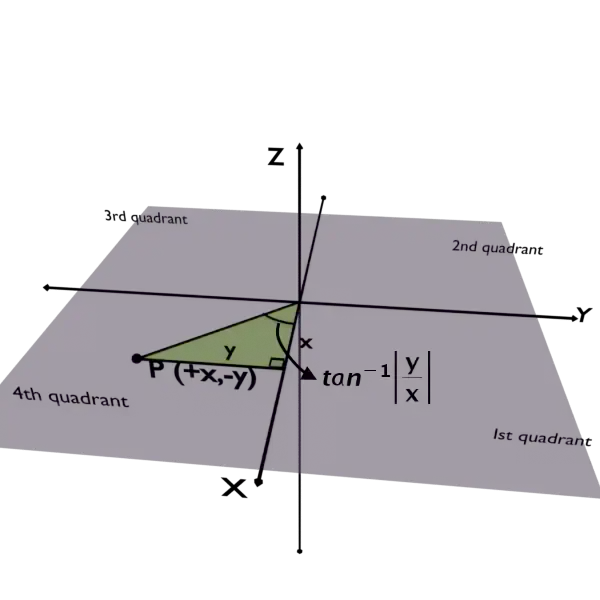
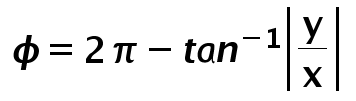
So, if you follow these steps, you will get your answer 100% correct everytime. Simple!
Do not forget to check our Awesome GATE courses.



