How to derive the Curl formula in Cylindrical and Spherical

Generally, we are familiar with the derivation of the Curl formula in Cartesian coordinate system and remember its Cylindrical and Spherical forms intuitively.

This article explains the step by step procedure for deriving the Deriving Curl in Cylindrical and Spherical coordinate systems.

What is Curl of Vector field?

Curl of a vector field is a measure of circulating nature or whirling nature of an vector field at the given point.

If the field lines are circulating around the given point leading to net circulation, signifies the Curl. The net circulation may be positive or negative. The uniform vector field posses zero curl.

You can refer this article for in depth discussion of the Curl.

Curl Formulas

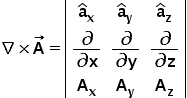
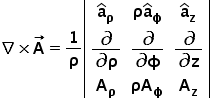
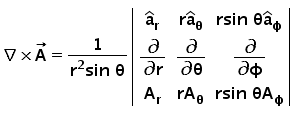
Deriving Curl in Cylindrical and Spherical

Let’s talk about getting the Curl formula in cylindrical first. Later by analogy you can work for the spherical coordinate system.

As read from previous article, we can easily derive the Curl formula in Cartesian which is as below.

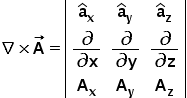
And the same in cylindrical coordinates is as follows: 

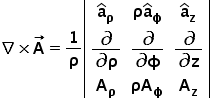
It is quite obvious to think that why some extra terms like (1/ρ) and ρ are present. Where do they come from? What is the logic behind them.

Because thinking intuitively, one might expect the formula similar to cartesian one.

We know, Cartesian is characterized by x, y and z while Cylindrical is defined by ρ, φ and z.

So one can think of getting partial derivatives w.r.t. ρ, φ and z instead of x, y and z and A_ρ, A_φ and A_z instead of A_x, A_y and A_z. Right?

The answer for this can be found in the steps for deriving the Curl in cylindrical system. So let us start.

Deriving the Curl in Cylindrical

We know that, the curl of a vector field A is given as,

\nabla\times\overrightarrow A

Here ∇ is the del operator and A is the vector field.

If I take the del operator in cylindrical and cross it with A written in cylindrical then I would get the curl formula in cylindrical coordinate system.

In cylindrical coordinates, any vector field is represented as follows:

\overrightarrow A=A_\rho{\overrightarrow a}\rho+A\phi{\overrightarrow a}_\phi+A_z{\overrightarrow a}_z

The Cylindrical del operator is as follows

\nabla={\overrightarrow a}\rho\frac\partial{\partial\rho}+{\overrightarrow a}\phi\frac1\rho\frac\partial{\partial\phi}+{\overrightarrow a}_z\frac\partial{\partial z}

Read this article to know how can we convert Del operator from Cartesian to Cylindrical.

So, let us take the cross product.

\nabla\times\overrightarrow A=\left({\overrightarrow a}\rho\frac\partial{\partial\rho}+{\overrightarrow a}\phi\frac1\rho\frac\partial{\partial\phi}+{\overrightarrow a}z\frac\partial{\partial z}\right)\times\left(A\rho{\overrightarrow a}\rho+A\phi{\overrightarrow a}_\phi+A_z{\overrightarrow a}_z\right) ={\overrightarrow a}\rho\times\frac\partial{\partial\rho}\left(A\rho{\overrightarrow a}\rho+A\phi{\overrightarrow a}\phi+A_z{\overrightarrow a}_z\right)+\frac1\rho{\overrightarrow a}\phi\times\frac\partial{\partial\phi}\left(A_\rho{\overrightarrow a}\rho+A\phi{\overrightarrow a}\phi+A_z{\overrightarrow a}_z\right)+{\overrightarrow a}_z\times\frac\partial{\partial z}\left(A\rho{\overrightarrow a}\rho+A\phi{\overrightarrow a}_\phi+A_z{\overrightarrow a}_z\right) ={\overrightarrow a}\rho\times\left[{\overrightarrow a}\rho\frac{\partial A_\rho}{\partial\rho}+A_\rho\frac{\partial{\overrightarrow a}\rho}{\partial\rho}+{\overrightarrow a}\phi\frac{\partial A_\phi}{\partial\rho}+A_\phi\frac{\partial{\overrightarrow a}_\phi}{\partial\rho}+{\overrightarrow a}_z\frac{\partial A_z}{\partial\rho}+A_z\frac{\partial{\overrightarrow a}_z}{\partial\rho}\right] +\frac1\rho{\overrightarrow a}\phi\times\left[{\overrightarrow a}\rho\frac{\partial A_\rho}{\partial\phi}+A_\rho\frac{\partial{\overrightarrow a}\rho}{\partial\phi}+{\overrightarrow a}\phi\frac{\partial A_\phi}{\partial\phi}+A_\phi\frac{\partial{\overrightarrow a}_\phi}{\partial\phi}+{\overrightarrow a}_z\frac{\partial A_z}{\partial\phi}+A_z\frac{\partial{\overrightarrow a}_z}{\partial\phi}\right] +{\overrightarrow a}z\times\left[{\overrightarrow a}\rho\frac{\partial A_\rho}{\partial z}+A_\rho\frac{\partial{\overrightarrow a}\rho}{\partial z}+{\overrightarrow a}\phi\frac{\partial A_\phi}{\partial z}+A_\phi\frac{\partial{\overrightarrow a}_\phi}{\partial z}+{\overrightarrow a}_z\frac{\partial A_z}{\partial z}+A_z\frac{\partial{\overrightarrow a}_z}{\partial z}\right]

Carefully observe that how derivative are written using the product rule.

Don’t consider unit vector to be a constant and taking out of the derivative. The derivatives of the unit vectors is not zero always. Check out this related article.

Let me represent the required derivatives of the unit vectors.

\frac\partial{\partial\rho}\left({\overrightarrow a}\rho\right)\;=0;\;\frac\partial{\partial\rho}\left({\overrightarrow a}\phi\right)=0;\;\frac\partial{\partial\rho}\left({\overrightarrow a}_z\right)=0 \frac\partial{\partial\phi}\left({\overrightarrow a}\rho\right)\;={\overrightarrow a}\phi;\;\frac\partial{\partial\phi}\left({\overrightarrow a}\phi\right)=-{\overrightarrow a}\rho;\;\frac\partial{\partial\phi}\left({\overrightarrow a}_z\right)=0 \frac\partial{\partial z}\left({\overrightarrow a}\rho\right)\;=0;\;\frac\partial{\partial z}\left({\overrightarrow a}\phi\right)=0;\;\frac\partial{\partial z}\left({\overrightarrow a}_z\right)=0

So putting all these derivatives in the step above, and taking the required cross product, we have,

\nabla\times\overrightarrow A=\frac{\partial A_\phi}{\partial\rho}{\overrightarrow a}z-\frac{\partial A_z}{\partial\rho}{\overrightarrow a}\phi-\frac1\rho\frac{\partial A_\rho}{\partial\phi}{\overrightarrow a}z+\frac{A\phi}\rho{\overrightarrow a}z+\frac1\rho\frac{\partial A_z}{\partial\phi}{\overrightarrow a}\rho+\frac{\partial A_\rho}{\partial z}{\overrightarrow a}\phi-\frac{\partial A\phi}{\partial z}{\overrightarrow a}_\rho

Collecting together the similar terms,

\nabla\times\overrightarrow A=\left(\frac1\rho\frac{\partial A_z}{\partial\phi}-\frac{\partial A_\phi}{\partial z}\right){\overrightarrow a}\rho+\left(\frac{\partial A\rho}{\partial z}-\frac{\partial A_z}{\partial\rho}\right){\overrightarrow a}\phi+\left(\frac{A\phi}\rho+\frac{\partial A_\phi}{\partial\rho}-\frac1\rho\frac{\partial A_\rho}{\partial\phi}\right){\overrightarrow a}_z

This can be adjusted and re written as like following,

\nabla\times\overrightarrow A=\frac1\rho\left[\left(\frac{\partial A_z}{\partial\phi}-\frac{\partial\left(\rho A_\phi\right)}{\partial z}\right){\overrightarrow a}\rho-\left(\frac{\partial A_z}{\partial\rho}-\frac{\partial A\rho}{\partial z}\right)\rho{\overrightarrow a}\phi+\left(\frac{\partial\left(\rho A\phi\right)}{\partial\rho}-\frac{\partial A_\rho}{\partial\phi}\right){\overrightarrow a}_z\right]

The above expression can be easily written in matrix determinant form as:

\nabla\times\overrightarrow A=\frac1\rho\begin{vmatrix}{\overrightarrow a}_\rho&\rho\overrightarrow a\phi&{\overrightarrow a}_z\\\frac\partial{\partial\rho}&\frac\partial{\partial\phi}&\frac\partial{\partial z}\\A_\rho&\rho A_\phi&A_z\end{vmatrix}

Which is our required curl formula in cylindrical. Similar steps can be followed for deriving the Divergence in Spherical.

Keep Learning! Keep Going!

Related Articles