While studying Electromagnetics or Electromagnetic Fields, the basics start with Gradient, Divergence, and Curl. Of course, you already know their formulae, but many times we need only the concept. Here, the Divergence of the vector field is defined in the simplest possible way that you will never forget.
Things we know about the Divergence of a Vector Field
⬤ It operates on ………..
Divergence operation operates on the vector field but the outcome is Scalar.
Read along or watch the video
⬤ The technical definition
The divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around a given point.
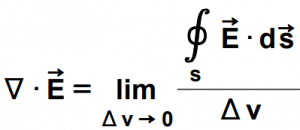
⬤ The Formulea in different Coordinate Systems
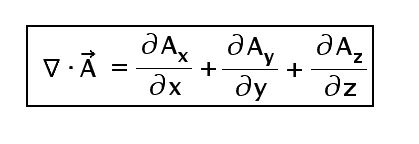
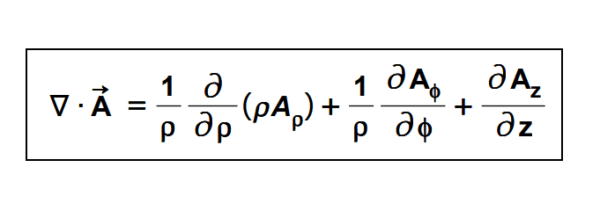
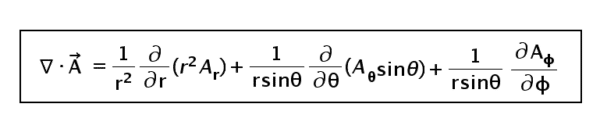
Divergence in simple words!
Divergence tells about the outgoingness of field lines
If at any point in the space, more and more field lines are coming out/sourcing out then we can say there is positive divergence.
If at any point in the space, more and more field lines are sinking into then we can say there is negative divergence.
Always remember, Divergence indicates the outgoingness nature of the field line at a particular point of space. More are field lines coming out, more is the divergence. Simple!
Do not forget to check our Awesome GATE courses.
