Almost all the Science Pupil are well aware of the term Integration. It is a common term in Mathematics. It also plays a very important role in the theory of Electromagnetics. In this article, I am going to discuss the formal meaning of integration and specifically what are Line, Surface and Volume Integrations and their significance in the Electromagnetics.
Line Integration in Electromagnetics
In Mathematics, formally the Integration gives the area under the curve. Consider the integration shown in the figure below.
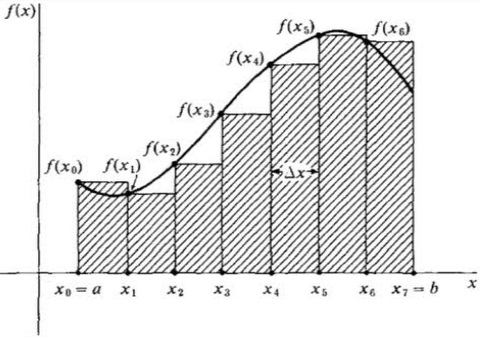
The differential or infinitesimal length is “dx” and corresponding to this small length an infinitesimal rectangular strip is shown. The area of this strip can be considered as multiplication of the value of f(x) at that x and length dx. In the process of integration, we add all such infinitesimal strips from A to B to give the area under the curve.
In Electromagnetics, we deal with various vector fields like Electric field, Magnetic field etc. Consider any such vector field E as shown in the following figure. Say, a line or vector AB is present within that field.
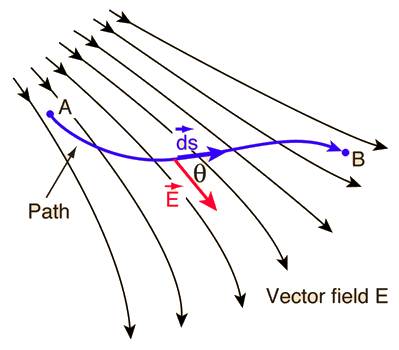
If we want the product of the length of the vector and component of the field along this vector (line) at every point of line then we write the integration as follows: –
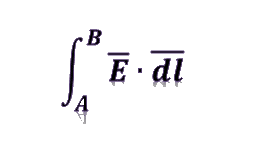
This integration is termed as a line integration.
The significance of Line Integration in Electromagnetics
The formula for work in Electromagnetics is based on the concept of line integration. Say we are moving a charge in the electric field, then work done is calculated by
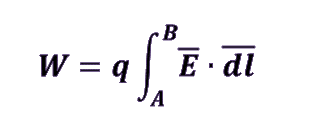
Basically, the line integration is required when we want to calculate the component or value of any vector field along the given vector path as in Ampere’s law.
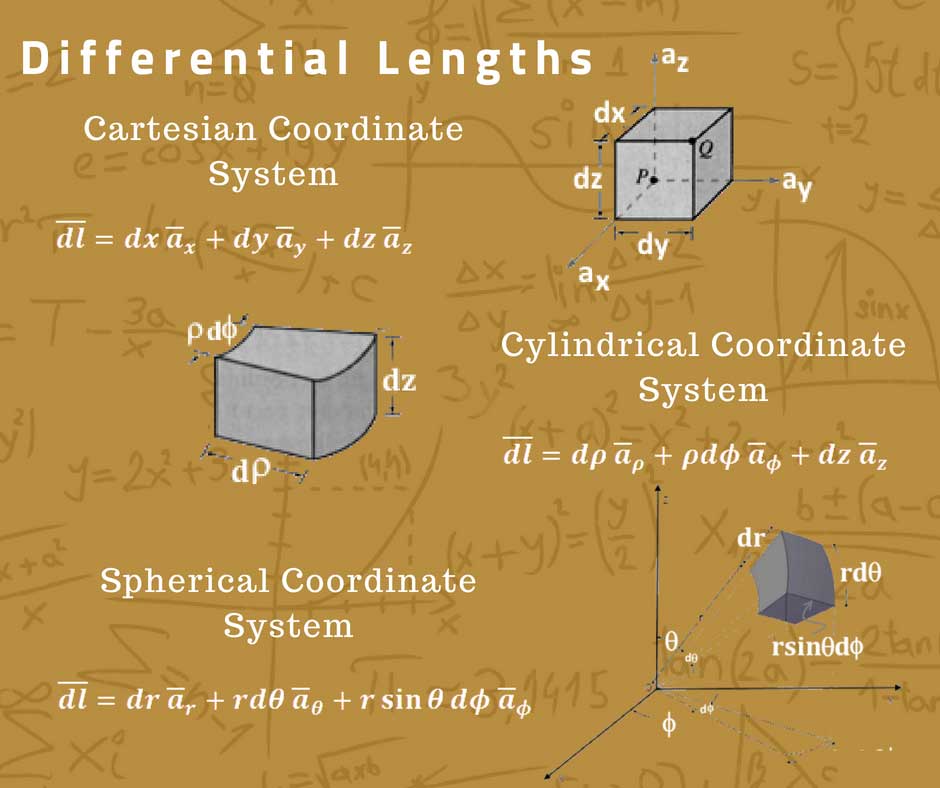
Different types of Differential lengths
In Electromagnetics we deal with Cartesian Coordinate System, Cylindrical Coordinate System, and Spherical Coordinate System. So the infinitesimal length “dl” should be defined in each of the coordinate systems. As we deal with vectors and vector fields in Electromagnetics, “dl” consists of infinitesimal change along each axis of the respective coordinate system.
Surface Integration in Electromagnetics
Consider any vector field A is present in the region. Let us say a surface of an area S is placed within the field as shown in the figure.
Now, the lines of the vector field will be passing through the surface. The total number of lines of the field that are passing through the given surface normally is termed as the flux of the field. And flux of the vector field through the given surface is represented by the surface integration.
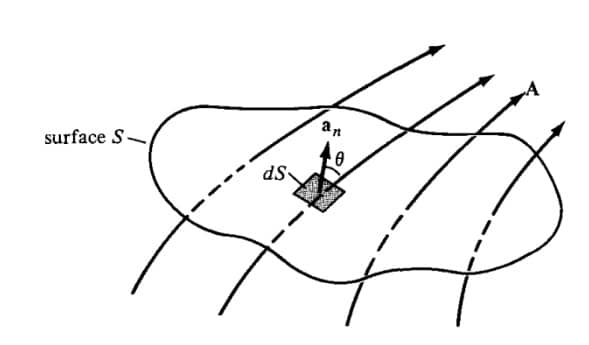
Representation of the Surface Integration
Surface integration is represented as shown below: –
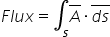
Where A is the vector field and ds is the infinitesimally small area from the given surface.
One point is worth noting here that in Electromagnetics, surface or plane is considered as a vector.
For example, let us say we have a square of side 10 cm. Then its area will be 100 cm2. So in the Electromagnetic Fields, this square will be represented by a vector of magnitude (length) 100 cm2 and direction normal (perpendicular) to the plane.
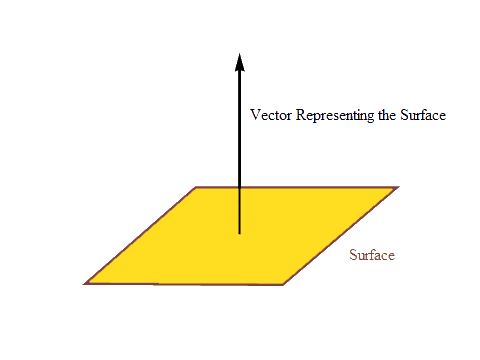
As stated above the surface integration gives us the flux of the vector field through the given surface. But in the process of integration, we first consider an infinitesimally small area or differential area from the given surface. As shown in the above representation diagram as ds.
As discussed just above ds would be the vector. So by taking dot product with ds vector, we will get the component of the field along the ds vector [by the definition of dot product]. As ds vector is already normal (perpendicular) to the surface, in other words, we get component of the field normal to the surface.
Then we sum up this product by covering all the ds present on the surface. This is represented by the integration sign in the representation. Actually, integration is the operation in which we sum up the effects of all the differential elements. As we cover all the differential elements i.e. ds, we have two variables changing to cover the complete area/surface. That means, in other words, when we say the surface integration we inherently mean the double integration.
Recall from the Electromagnetics Basics Course for a surface or plane two coordinates are variable and rest is constant.
As surface integration require double integrations, it can also be represented as: –
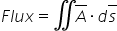
Differential surface (ds) in different Coordinate Systems
We already know, in Electromagnetics, we use Rectangular, Cylindrical, and Spherical Coordinate Systems. So we must define differential element ds for each of them as shown.
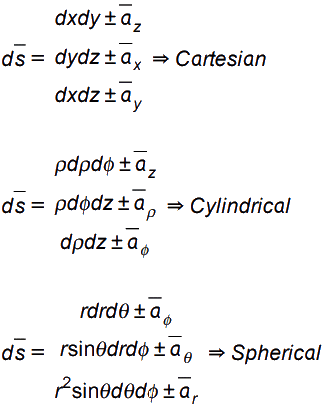
Volume Integration in Electromagnetics
Consider any object having volume say for example a solid metal sphere. Let us assume that its density is ρ kg/m3 and volume is V m3. If we are asked to calculate the mass of this sphere, we can calculate quickly as-
Mass = Density × Volume = ρV Kg
Now let us have a twist. Assume that density ρ is given as the certain function of coordinates of the point which you are considering. This case wouldn’t be so easy as above and we cannot conclude our answer of mass merely by multiplying the density function with the volume. At every small point of the given volume, the density must be calculated at that point and multiplied with infinitesimal volume around that point.

In other words, to find the mass in the latter case, we have to use the integral calculus by finding the infinitesimal mass by considering the infinitesimal volume and collecting all such infinitesimal pieces all over the volume of sphere i.e. taking integration.
This type of integration is called volume integration.
Representation of the Volume Integration
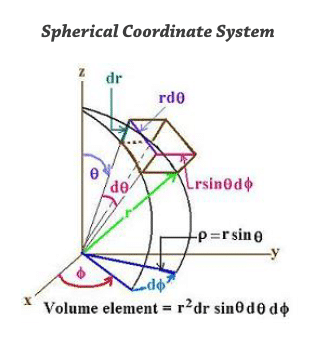
Volume integration is represented as shown below-
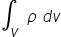
where ρ is the scalar function distributed over the volume like density, volume charge density etc. and dv is the infinitesimal/ differential volume for the given ranges of variables.
Now as explained in line and surface integration, volume integration can be understood as:-
Calculating the infinitesimal product of the scalar function at a point and small (infinitesimal) volume around that point. Then summing up all such infinitesimal products covering all the volume.
Now we know that to have a volume or to cover the complete volume, all three coordinates must be covered. In other words, the integration would be the triple integration covering the range for each variable. so it is also represented as-
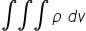
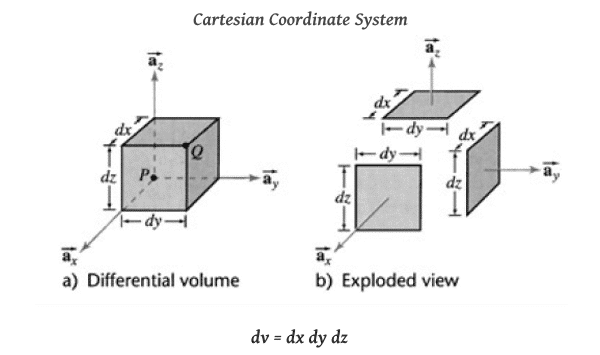
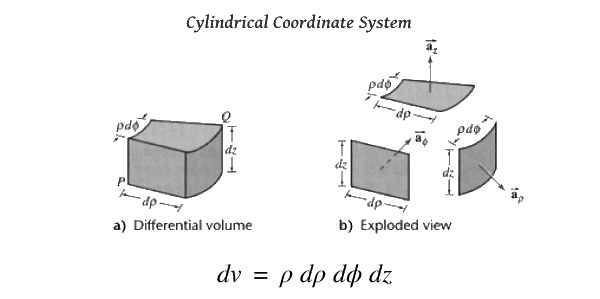
Differential volume (dv) in different Coordinate Systems
In every coordinate system, the small or differential volume is obtained by multiplying all three differential lengths.
Can volume integration be calculated for vector field?
Volume on its own is a scalar quantity and volume integrations are mainly calculated for scalar functions like density, volume charge density, temperature etc. But it can also be calculated for vector functions by considering each component separately.
Do not forget to check our Awesome GATE courses.