What is a Cylindrical Coordinate System?

Cylindrical Coordinate System is widely used in Engineering and Science studies. In this article, let us revive it from the point of view of Electromagnetics.

Spatial variations i.e. variations in space requires unique representation of a point of interest using suitable reference. Such reference systems are called as coordinate systems. Coordinate system can be orthogonal or non-orthogonal coordinate system. An orthogonal system is one in which the coordinates arc mutually perpendicular. The non-orthogonal coordinate system is hard to work on and practically neglected.

There are many types of orthogonal coordinate systems as a Cartesian coordinate system, Circular Cylindrical, Spherical, Elliptic Cylindrical, Parabolic Cylindrical, Conical, Prolate Spheroidal, Oblate Spheroidal and ellipsoidal.

What are Cylindrical Coordinates?

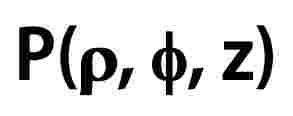
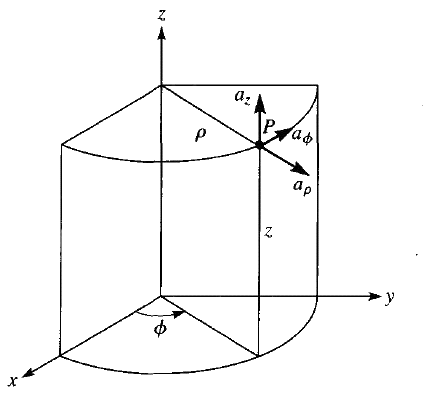
ρ is the radius of the cylinder passing through P or the radial distance from the z-axis.
φ is called as the azimuthal angle which is angle made by the half-plane containing the required point with the positive X-axis.
z coordinate is the same as in the Cartesian system; it is the distance of the required point from the XY plane.

The Cylindrical Frame of Reference

Rho (ρ) Coordinate

Consider that P is any point present in the space. Assume the coordinate axes same as the Cartesian Coordinate System as the reference. Then the distance of this point P, radial distance, from the Z-axis is termed as the rho (ρ) coordinate.

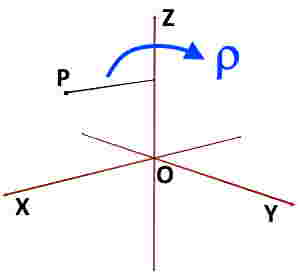
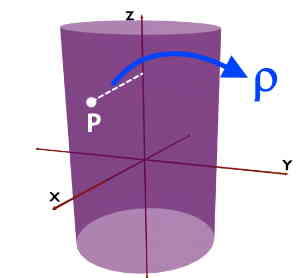
It is also defined as the radius of the imaginary cylinder about Z-axis that is assumed to be passing through the given point.

Range of Rho (ρ) Coordinate

Rho (ρ) coordinate of the Cylindrical Coordinate System can take any value from 0 to ∞.

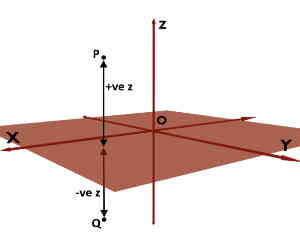
Points can be present anywhere in the space. And rho coordinate of any point is the radial distance from Z-axis. For example, consider two points P and Q whose rho coordinates are shown in the figure.

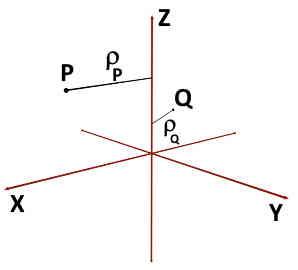
So obviously, at the maximum, point can be at infinity. And at the minimum, point can be present on the Z-axis having ZERO radial distance.

Note that, Rho (ρ) coordinate can never be negative because it’s a distance of the given point from the Z-axis. There is not positive or negative side as we have seen in Cartesian Coordinates. Actually, it’s a radius of the imaginary cylinder passing through the given point. And it can never be negative.

Phi (ϕ) Coordinate

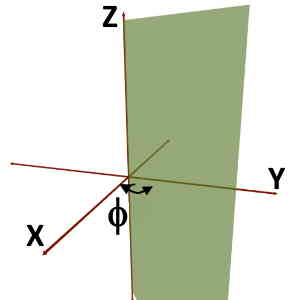
Again, consider any point P in the space. Imagine that you are constructing a plane stuck to Z-axis so that it would pass through the given point, P. Such imaginary plane is called as a vertical half plane. And angle made by this half plane with the +X axis is the Phi (ϕ) coordinate of the Cylindrical Coordinate System.

When do we take Phi (ϕ) negative?

Watch: When do we take phi negative in Cylindrical Coordinate System?

Remember that, an angle made by the vertical half plane with the +X axis is the Phi (ϕ) coordinate. But, which way should trace this angle?

For example, consider the point P present in space. Now to define Phi of this point P, we would need vertical half plane. A vertical half plane is an imaginary plane stuck to Z-axis so that it would pass through the given point i.e. P. It is shown by green in the following figures. The angle made by this vertical half plane with the +X axis is the Phi (ϕ) coordinate.

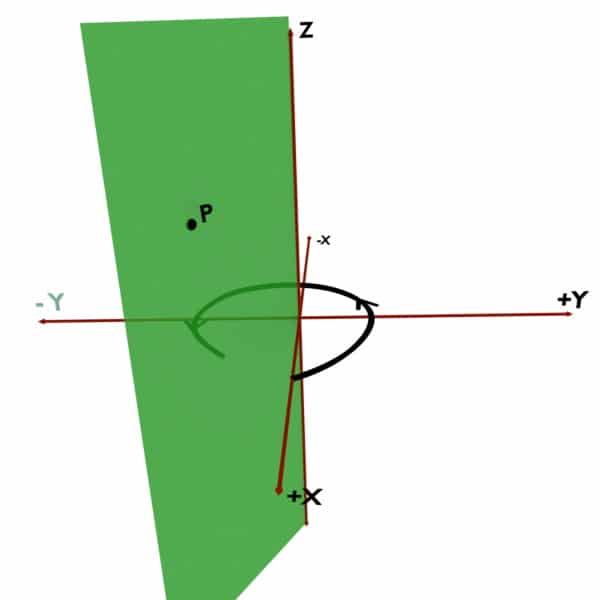
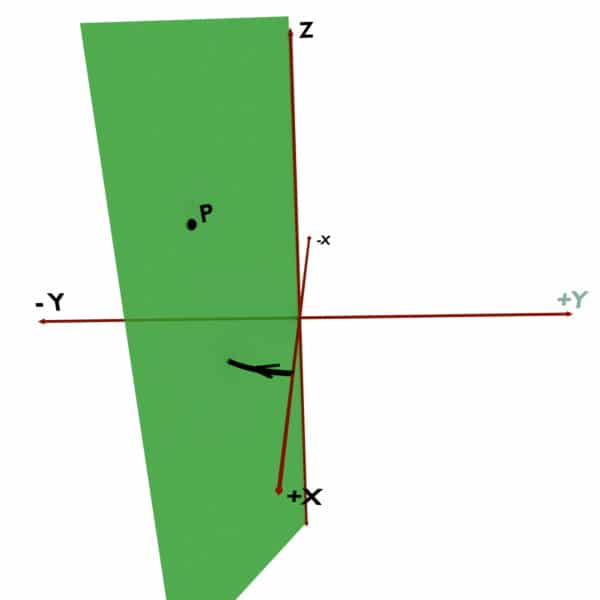
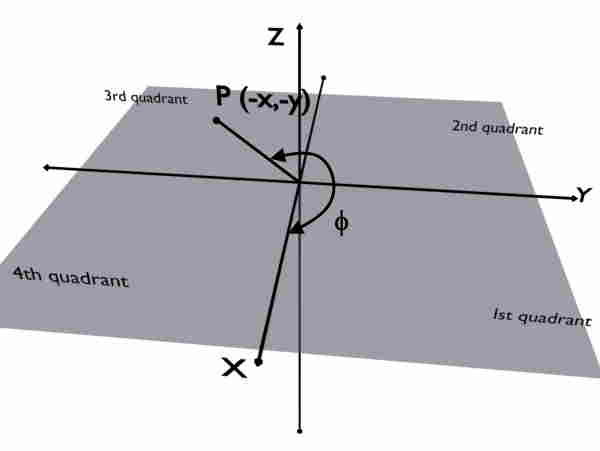
Now the problem is, how should we take this angle? Should we trace it in anticlockwise direction as shown in first diagram? Or should we trace it in clockwise direction as shown in second diagram?

So remember that, according to Cylindrical Coordinate System’s convention, Phi (ϕ) must be traced in Anticlockwise direction. That is, your path of tracing should be along +X to +Y to -X to -Y to +X.

And, if you trace the angle in clockwise direction viz. along +X to -Y to -X to +Y to +X, then you take Phi (ϕ) NEGATIVE.

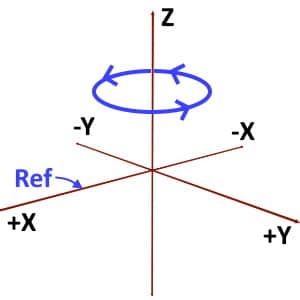
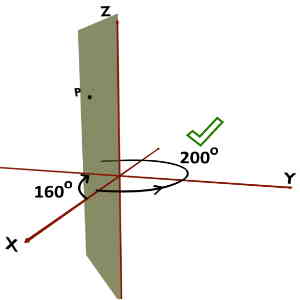
For example, consider a point P and the vertical half plane containing it. This plane makes angle 300^o if traced in the anticlockwise direction and 160^o if traced in clockwise direction. So, the correct Phi(ϕ) would be 300^o or -160^o.

Range of Phi (ϕ) coordinate.

Phi coordinate is an angle and it can take any value between 0^o to 360^o.

Point can be present anywhere in the space. And the vertical half plane stuck to the Z axis, to contain that point, could have any orientation within 360 degrees.

Hence, Phi can take any value between 0^o to 360^o or 0 to 2π.

z Coordinate

It is exactly same as the z-coordinate of the Cartesian Coordinate System. Actually, it is borrowed from there.

z-coordinate is the perpendicular distance of the required point from the XY plane. As we know from the Cartesian System, it can take any value between -∞ to +∞.

Constant Coordinate Surfaces

In Cartesian Coordinate System, we observed that, locus of any one coordinate as a constant, is a surface or plane. Similarly, is the case with Cylindrical Coordinate System. Any one coordinate as a constant while other two variables, would lead to a surface or plane.

Rho (ρ) = constant Surface

Assume that we are given with ρ = 3 while ϕ and z coordinates can take any value.

We are given with ρ coordinate equal to 3 i.e. ρ = constant and no restrictions over the values of y and z coordinates. So, just apply the definition of ρ coordinate. It is the radial distance from Z axis. And, in this case we want locus of all such points which are at radial distance of 3 units from the Z-axis. So, its locus lead to a curved cylindrical surface with radius 3 units, as shown in the figure.

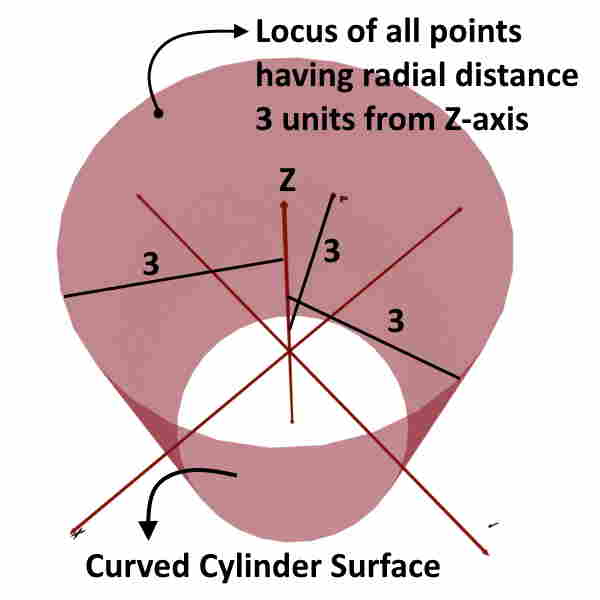
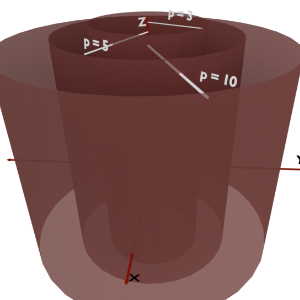
So, locus of ρ = constant is a curved cylindrical surface of radius equal to that ρ.

Phi (ϕ) = constant Surface

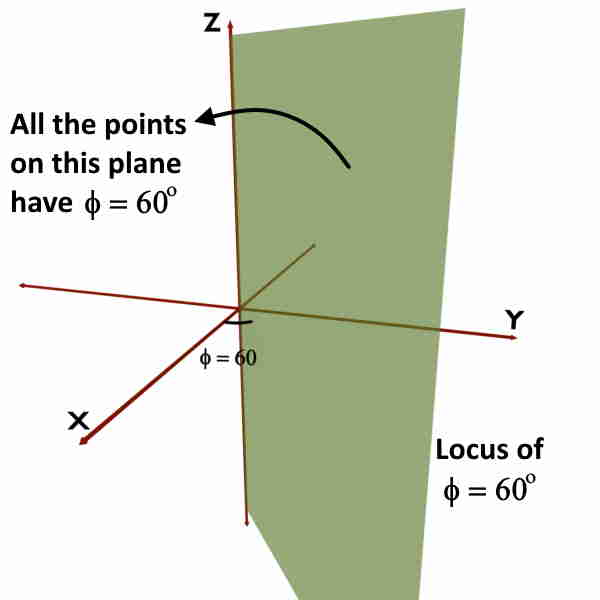
Assume that we are given with ϕ = 60^o while ρ and z coordinates can take any value.

We are given with ϕ coordinate equal to 60^o i.e. ϕ = constant and no restrictions over the values of ρ and z coordinates. So, just apply the definition of ϕ coordinate. It is the angle made by the vertical half plane containing the given point with +X.

So obviously, all the points which are present on the same vertical half plane, would have same ϕ coordinate i.e. ϕ = 60^o. In other words, locus of ϕ = 60^o will be the vertical half plane as shown in figure.

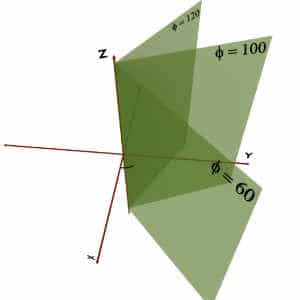
So, locus of ϕ = constant is a vertical half plane stuck to the Z axis making an angle ϕ with the +X axis.

z = constant Surface

And, in Cartesian Coordinate System, we have seen that z = constant is a surface/plane parallel to XY plane present at given z.

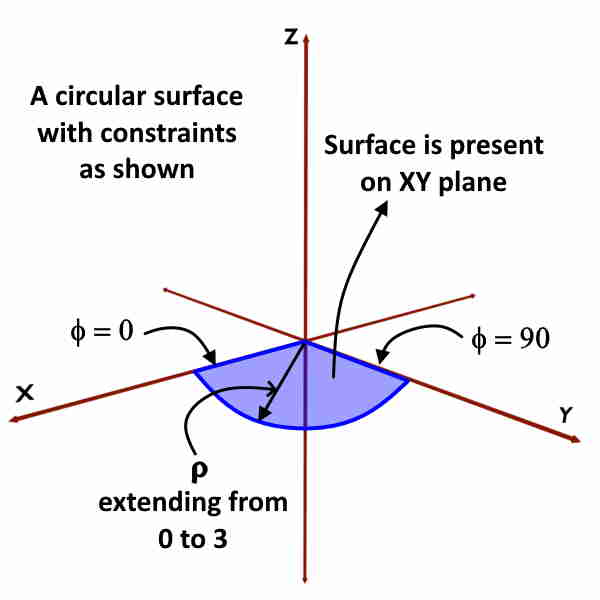
Can you locate, 0<ρ<3; 0<ϕ<90^o ; z=0 ?

We know that z = constant is a plane or surface parallel to XZ plane. So z = 0 will be itself a XY plane.

But here ρ and ϕ coordinates are not completely “Don’t cares”. But we are given with their ranges.

So the plane or surface will not be infinite one but only extended up to the given range of ρ and ϕ.

Lines in Cylindrical System

What would be locus if we are given with two coordinates constants & remaining one variable?

Simple! It would be a line. We know that single coordinate as a constant leads to a surface. So, two coordinates constants would lead to two surfaces. And, the intersection of these two surfaces/planes would be our required locus i.e. line.

Rho (ρ) = constant & Phi (ϕ) = constant

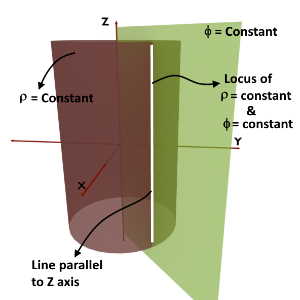
Rho (ρ) = constant is a curved cylindrical surface while Phi (ϕ) = constant is a vertical half plane. So, intersection of these two planes is a line parallel to Z-axis.

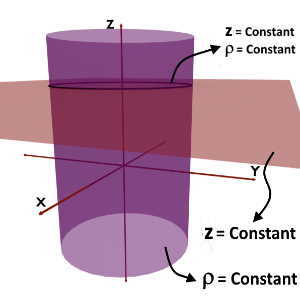
Rho (ρ) = constant & z = constant

Rho (ρ) = constant is a curved cylindrical surface while z = constant is a plane parallel to XY plane. So, intersection of these two planes is a line along Phi i.e. circular line.

Phi (ϕ) = constant & z = constant

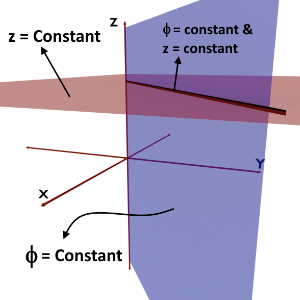
Phi (ϕ) = constant is a vertical half plane while z = constant is a plane parallel to XY plane. So, intersection of these two planes is a line along Rho i.e. radial line.

So remember that if two coordinates are given as constants and remaining one is a variable then the locus is a line along the variable coordinate.

Also remember that, if range of the variable coordinate is not given then the line would be infinite. And if the range is mentioned then line would be finite.

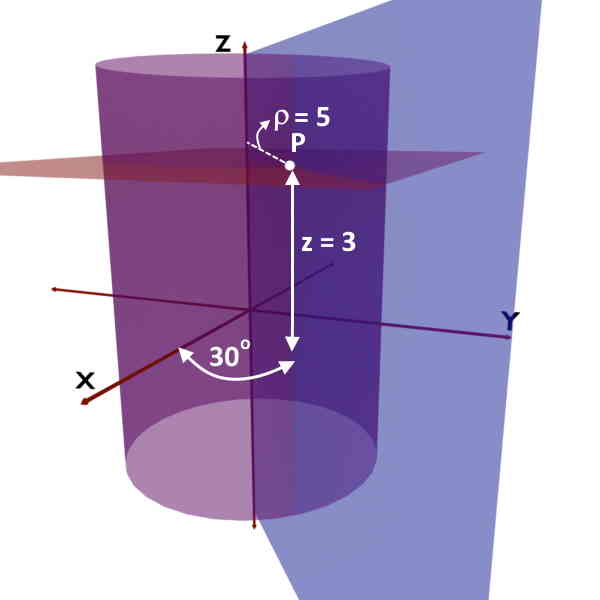
What if all the coordinates are constants or given?

Assume that a point in space is P (5, 30^o, 3). That is, ρ-coordinate = 5; ϕ-coordinate = 30^o; z-coordinate = 3.

In simple words, this point P is at a radial distance of 5 units from Z-axis. Or it is present on the surface of imaginary cylinder centered at Z-axis with radius 5. It is on a plane, called as vertical half plane making an angle 30^o with the +X axis. Also, it is 3 units above the XY plane. And the common intersection of all these planes, is our point P, uniquely located in the space.

How are vectors represented in the Cylindrical Coordinate System?

The general way of representation for the vectors is as follows:

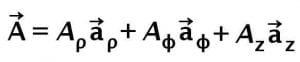
A_ρ , A_ϕ and A_z are the Rho, Phi and Z components of the vector while a_ρ , a_ϕ and a_z are the unit vectors of Cylindrical Coordinate System.

How are the Unit Vectors defined for a Cylindrical Coordinate System?

Watch: How are Unit vectors defined in Cylindrical Coordinates to represent any Vector in Space?

Any vector in a Cylindrical coordinate system is represented using three mutually perpendicular unit vectors.

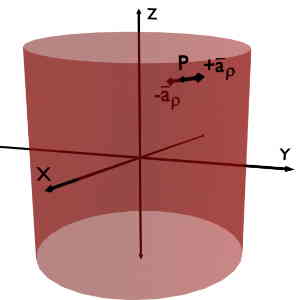
Unit vector ${\overrightarrow a}_\rho$ at the given point P, is the vector of unit magnitude; perpendicular to Rho = constant plane and pointing in the increasing rho direction.

While $-{\overrightarrow a}_\rho$ is the vector of unit magnitude; perpendicular to rho = constant plane and pointing in the decreasing rho direction.

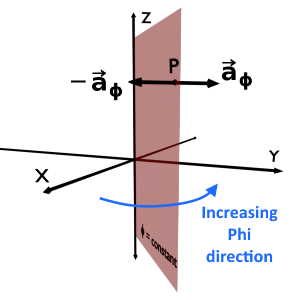
Unit vector ${\overrightarrow a}_\phi$ at the given point P, is the vector of unit magnitude; perpendicular to Phi = constant plane and pointing in the increasing phi directioni.e. anticlockwise.

While $-{\overrightarrow a}_\phi$ is the vector of unit magnitude; perpendicular to phi = constant plane and pointing in the decreasing phi direction.

Unit vectors $\pm{\overrightarrow a}_z$ are same as the Cartesian Coordinate System viz. perpendicular to z = constant plane at given point.

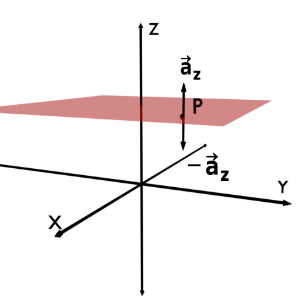
So, any vector in Cylindrical Coordinate System, is a combination or vector addition of rho component, phi component and z component presented by unit vectors $\pm{\overrightarrow a}_\rho$ , $\pm{\overrightarrow a}_\phi$ and $\pm{\overrightarrow a}_z$ respectively.

Conversion of a Point between Cylindrical and Cartesian

We know that any point or vector in space can be represented using different coordinate systems viz. Cartesian, Cylindrical or Spherical. But keep in mind that we are representing the same point/vector using different conventions.

We use the Coordinate System according to need of our EMT problem. So, there are many instances in Electromagnetics, when you need to convert from one coordinate system to other or vice-versa.

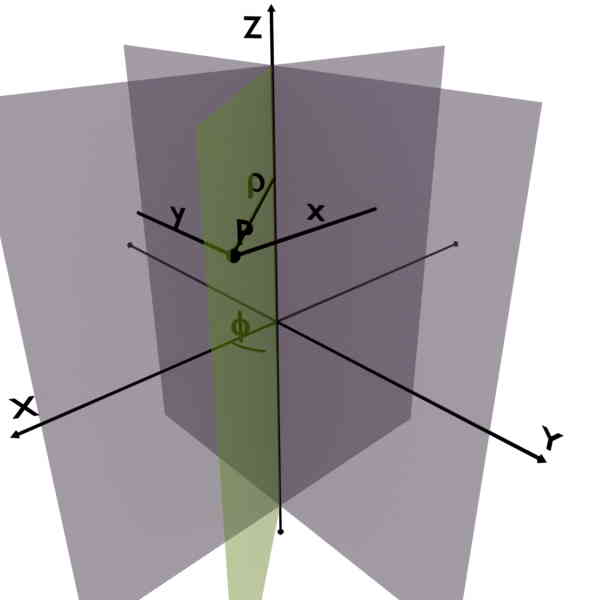
Let us say we are given with the point P in space. Now in Cartesian Coordinate System coordinates of point P are (x, y, z). x is the perpendicular distance from YZ plane, y is the perpendicular distance from XZ plane and z is the perpendicular distance from XY plane.

At the same time, given point P can also be represented using Cylindrical Coordinate System with coordinates P (ρ, ϕ, z). ρ is the radial distance from Z-axis, ϕ is the angle made by vertical half plane with +X axis and z, same as Cartesian.

And now let us draw coordinates for both of these in a single diagram. Note that z-coordinate in both the systems are exactly the same hence we’ve not shown in the figure.

From figure above, we can easily get the relation between Cartesian and Cylindrical coordinates.

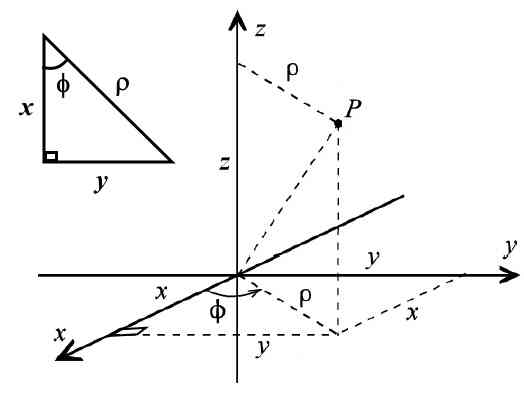
From Cartesian to Cylindrical

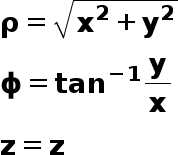
From Cylindrical to Cartesian

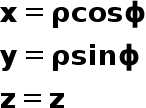
Example: Represent P(1, 1, 3) into Cylindrical

Given point is P(1, 1, 3) i.e. represented in Cartesian Coordinate System. And we are asked to represent it in Cylindrical.

In Cartesian, any point is represented as (x, y, z). Hence, For point P, x = 1; y = 1 and z = 3.

Hence, $\rho=\sqrt{x^2+y^2}=\sqrt{1^2+1^2}=\sqrt2$

And, $\phi=\tan^{-1}\left(\frac yx\right)=\tan^{-1}\left(\frac11\right)=45^\circ$

Hence, $P(1,1,3)\equiv P(\sqrt2,45^\circ,3)$

Example: Represent A(-1, -1, 3) into Cylindrical

Same as above, x = -1; y = -1 and z = 3.

Hence, $\rho=\sqrt{x^2+y^2}=\sqrt{(-1)^2+(-1)^2}=\sqrt2$

And, $\phi=\tan^{-1}\left(\frac yx\right)=\tan^{-1}\left(\frac{-1}{-1}\right)=45^\circ$

Now here is the PROBLEM! This can not be correct. We got Phi for (-1, -1, 3) and Phi for (1, 1, 3) exactly the same. And it is not at all possible. Why? Because, both the point are different points, in different quadrants. So, their phi coordinate cannot be the same.

Then, what happened? Here, we need slight modification to the formula for PHI, while obtaining from Cartesian. Let us discuss this in following section.

The problem of PHI in Cylindrical-Cartesian conversion

Watch: Problem of Phi while converting a Point from Cartesian to Cylindrical Coordinate System.

There is absolutely no problem if the required point is in first quadrant i.e. if point is having both the coordinates x and y as positive.

For example consider the following illustration where point P is in 1st quadrant say x = 1 and y = 1. We know that z coordinate is exactly same in both the coordinate systems, so don’t worry about z. Anyway we only want x and y coordinates for calculating phi.

So, the required angle phi is shown in the figure. It is the measured with +X axis isn’t it?

So with the conversion formula, we would get the correct answer. No problem!!

\phi=\tan^{-1}\left(\frac11\right)=45^\circ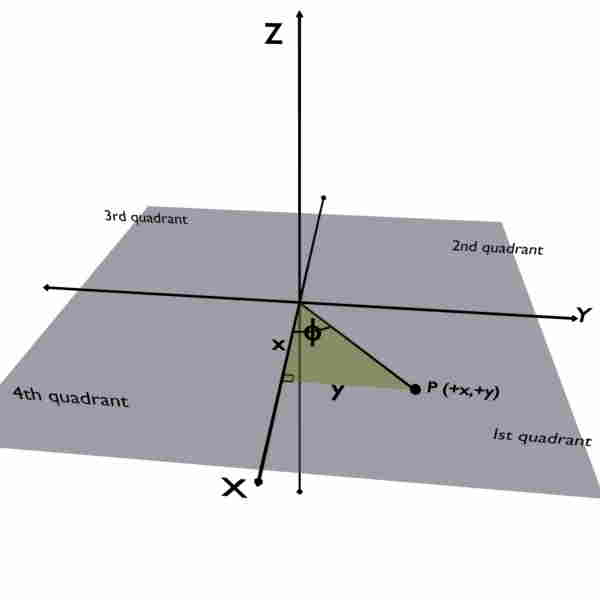

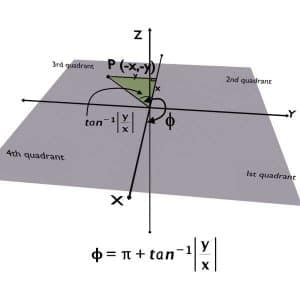
But now consider that the given point P is in the third quadrant i.e. x and y coordinates both are negative.

Say, coordinates of P are x = – 1 and y = – 1. Now the required phi is shown in the figure.

We know that, PHI is always measured w.r.t. +X axis. So you can easily observe that the phi for such point in the third quadrant is obviously greater than 180^o.

But if you apply the formula to calculate this phi we will still get 45^o.

\phi=\tan^{-1}\left(\frac{-1}{-1}\right)=45^\circ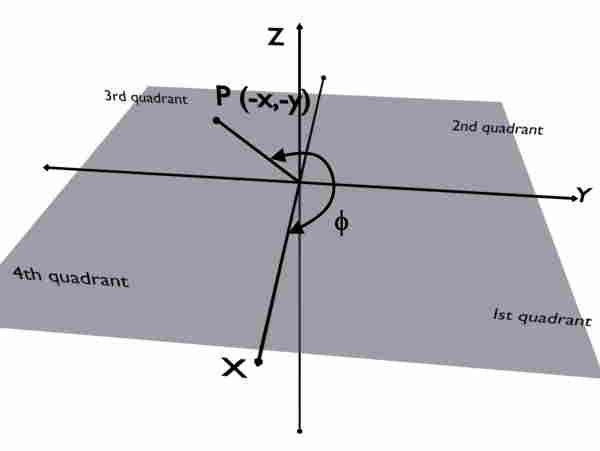

Actually, the formula gives us the minimum angle inscribed by the y and x.

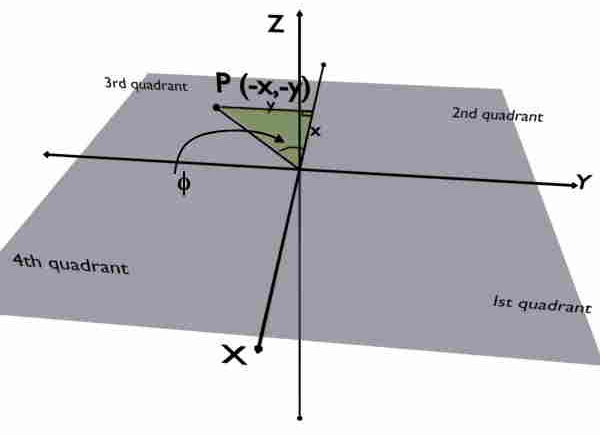
So obliviously, to get the correct phi in this case we have to add 180 or π to the answer of that formula, isn’t it? Similar problem appear while converting the points presents in 2^nd and 4^th quadrants.

So, to overcome such problems, we insert a mod into the formula and then manually add or subtract certain angle based on the quadrant of the given point. This is shown in the image.

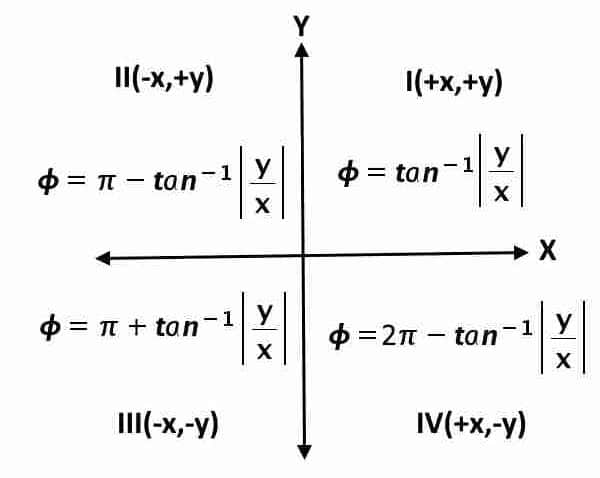
As said before, there is absolutely no problem if the required point is in first quadrant i.e. if point is having both the coordinates x and y as positive.

If the given point is lying in the second quadrant then x is negative while y is positive.

So, the required Phi would be angle obtained after substracting the formula angle from 180 or π.

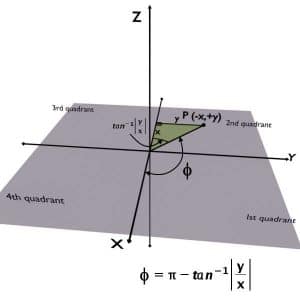
If the given point is lying in the third quadrant then x and y both are negative.

So, the required Phi would be angle obtained after summing the formula angle with 180 or π.

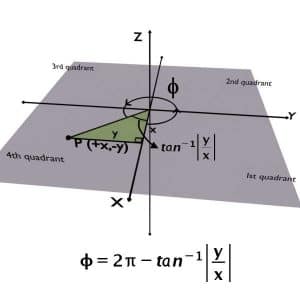
If the given point is lying in the fourth quadrant then x is positive and y is negative.

So, the required Phi would be angle obtained after substracting the formula angle from 360 or 2π.

Conversion of a Vector between Cylindrical and Cartesian

For Cartesian Coordinate System, the general way of representation for the vectors is as follows:

\overrightarrow A=A_x{\overrightarrow a}_x+A_y{\overrightarrow a}_y+A_z{\overrightarrow a}_z

Ax , Ay and Az are the X, Y and Z components of the vector while ax , ay and az are the unit vectors of Cartesian Coordinates.

For Cylindrical Coordinate System, the general way of representation for the vectors is as follows:

\overrightarrow A=A_\rho\overrightarrow a\rho+A\phi{\overrightarrow a}_\phi+A_z{\overrightarrow a}_z

Aρ , Aϕ and Az are the Rho, Phi and Z components of the vector while aρ , aϕ and az are the unit vectors of Cylindrical Coordinate System.

To convert the representation of the given vector from Cartesian to Cylindrical or vice-versa, we should know the relation between their unit vectors. Let us discuss this in following section.

Relation between Cartesian and Cylindrical Unit Vectors

We know that, unit vector a_z is common in both the systems. So, let us not consider them in this discussion.

For Cartesian Coordinate System, unit vector a_x is along the +X direction while unit vector a_y is along the +Y direction.

For Cylindrical Coordinate System, unit vector a_ρ is normal to rho = constant plane and along increasing rho direction. While unit vector a_ϕ is normal to phi = constant plane and along increasing phi direction i.e. anticlockwise.

We can draw unit vectors of both these system together with a common scale, as shown in figures.

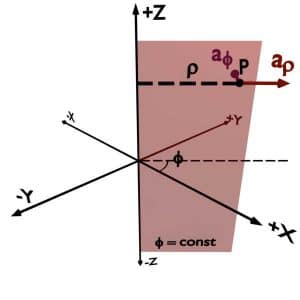
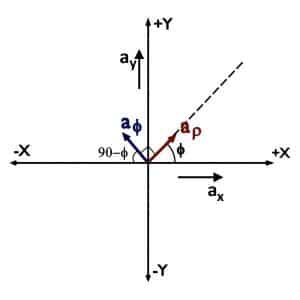
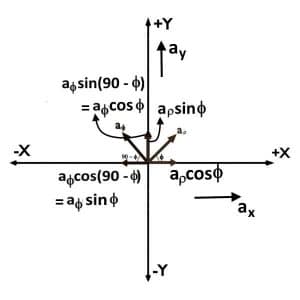
We can easily decompose the unit vectors a_ρ and a_ϕ along X and Y to obtain their relation with Cartesian Unit vectors.

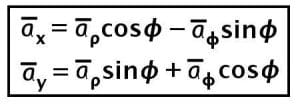
So, these are the expressions for Cartesian unit vectors in terms of Cylindrical unit vectors.

You can also decompose unit vectors a_x and a_y along a_ρ and a_ϕ to get the expressions for Cylindrical unit vectors in terms of Cartesian unit vectors.

Relation between Cartesian and Cylindrical Vectors

Let us say we are given with vector $\overrightarrow A=A_x{\overrightarrow a}_x+A_y{\overrightarrow a}_y+A_z{\overrightarrow a}_z$ which is represented with Cartesian Coordinate System and we wish to represent the same vector with Cylindrical Coordinate System.

Now, we have the relation between cartesian and cylindrical unit vectors.

\overrightarrow A=A_x({\overrightarrow a}_\rho\cos\phi-{\overrightarrow a}_\phi\sin\phi)+A_y({\overrightarrow a}_\rho\sin\phi-{\overrightarrow a}_\phi\cos\phi)+A_z{\overrightarrow a}_z

Arranging the terms, we have,

\overrightarrow A=(A_x\cos\phi+A_y\sin\phi){\overrightarrow a}_\rho+(-A_x\sin\phi+A_y\cos\phi){\overrightarrow a}_\phi+A_z{\overrightarrow a}_z

But, in Cylindrical Coordinate System, general form of the vector is,

\overrightarrow A=A_\rho{\overrightarrow a}_\rho+A_\phi{\overrightarrow a}_\phi+A_z{\overrightarrow a}_z

So, we have,

$A_\rho=A_x\cos\phi+A_y\sin\phi$ ,

$A_\phi=-A_x\sin\phi+A_y\cos\phi$ ,

$A_z=A_z$ ;

This can be easily memorized in the matrix form as follows,

\begin{bmatrix}A_\rho\\A_\phi\\A_z\end{bmatrix}=\begin{bmatrix}\cos\phi&\sin\phi&0\\-\sin\phi&\cos\phi&0\\0&0&1\end{bmatrix}\begin{bmatrix}A_x\\A_y\\A_z\end{bmatrix}

So, this matrix should be remembered for obtaining the components of the vector in Cylindrical Coordinate system if we already have the components in Cartesian.

Had we started in reverse order i.e. representing the vector in Cylindrical into the Cartesian, we have got transpose of the above matrix.

Hence, the transformations of the vector from one to other (Cartesian system and Cylindrical system) is given as-

Example: Represent A = 2a_x+a_y+5a_z into Cylindrical Coordinates.

Comparing with, $\overrightarrow A=A_x{\overrightarrow a}_x+A_y{\overrightarrow a}_y+A_z{\overrightarrow a}_z$

$A_x=2;\;A_y=1;\;A_z=5$ ,

Now, we want cylindrical components,

\begin{bmatrix}A_\rho\\A_\phi\\A_z\end{bmatrix}=\begin{bmatrix}\cos\phi&\sin\phi&0\\-\sin\phi&\cos\phi&0\\0&0&1\end{bmatrix}\begin{bmatrix}A_x\\A_y\\A_z\end{bmatrix}

\begin{bmatrix}A_\rho\\A_\phi\\A_z\end{bmatrix}=\begin{bmatrix}\cos\phi&\sin\phi&0\\-\sin\phi&\cos\phi&0\\0&0&1\end{bmatrix}\begin{bmatrix}2\\1\\5\end{bmatrix}

$A_\rho=2\cos\phi+sin\phi$ ,

$A_\phi=-2\sin\phi+\cos\phi$ ,

$A_z=5$ ,

In Cylindrical Coordinates,

\overrightarrow A=A_\rho{\overrightarrow a}_\rho+A_\phi{\overrightarrow a}_\phi+A_z{\overrightarrow a}_z

\overrightarrow A=(2\cos\phi+sin\phi){\overrightarrow a}_\rho+(-2\sin\phi+\cos\phi){\overrightarrow a}_\phi+5{\overrightarrow a}_z

Further, if specific point is given, then we can find sinϕ and cosϕ to get the specific vector at that point.

Hope you enjoyed the article. Amplify your concepts by sharing with others.

Do not forget to check our Awesome GATE courses.

GATE-EC

GATE-EE