Cartesian Coordinate System is widely used in Engineering and Science studies. In this article, let us revive it from the point of view of Electromagnetics.
Coordinate System
Most of the quantities that we deal in Electromagnetics are functions of both space and time. Variations in space are represented with the proper coordinate system.
Electromagnetics is the study of phenomena related to Electric field, Magnetic field, their interaction etc. These quantities are time-varying as well as spatial functions. In order to describe spatial variations of these quantities, one must be able to define all points and vectors uniquely in space in the appropriate manner.
A point can be represented using orthogonal or non-orthogonal coordinate system. An orthogonal system is one in which the coordinates arc mutually perpendicular. The non-orthogonal coordinate system is hard to work on and practically neglected.
There are different types of orthogonal coordinate systems- Cartesian (or rectangular), circular cylindrical, spherical, elliptic cylindrical, parabolic cylindrical, conical, prolate spheroidal, oblate spheroidal and ellipsoidal.
What are the Cartesian Coordinates?
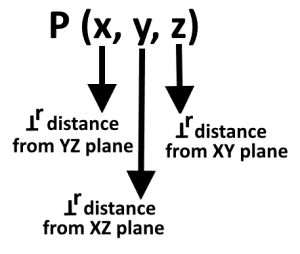
Any point of the space is represented using three coordinates: x, y, and z which are the distances measured from reference planes formed by the three coordinate axes viz. X-axis, Y-axis, and Z-axis. The x-coordinate is the perpendicular distance from the YZ plane. The y-coordinate is the perpendicular distance from the XZ plane, similarly, z-coordinate is the normal distance from XY plane.
The Cartesian Frame of Reference
Reference Frame for Cartesian Coordinate System is a set of three mutually perpendicular lines called as X, Y and Z axes with intersection point called as Origin. Any point in the space is then located with set of THREE distances from the reference planes XY, YZ and XZ.
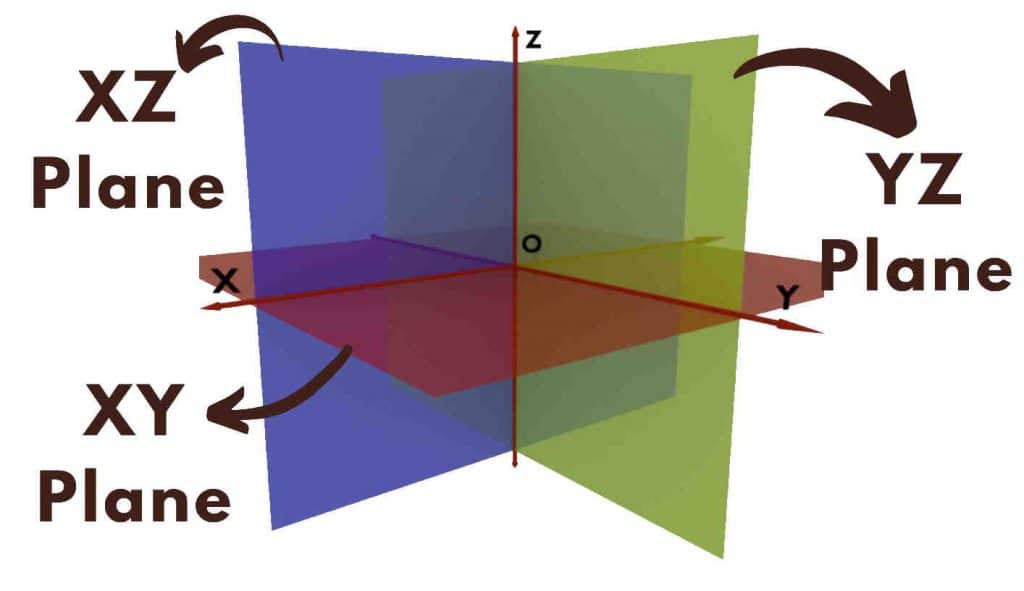
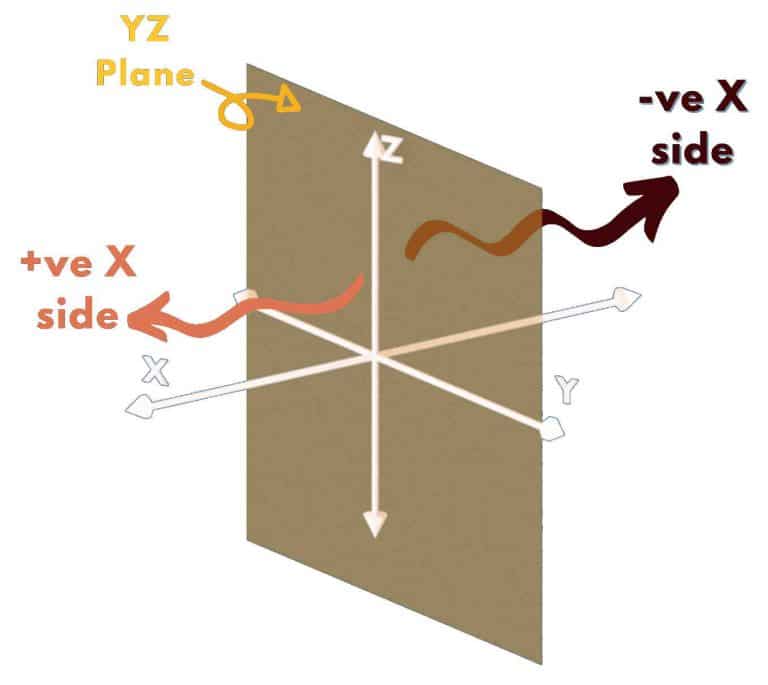
A Reference Plane divides the space along respective Axis into TWO parts POSITIVE and NEGATIVE.
For example YZ plane is the plane containing Y axis and Z axis. And the points which lie in the positive X side will have positive x-coordinate. While the points in the space present on the negative X side will have negative x-coordinate as shown in the following figure.
Likewise XY plane divides space into +z and -z side. And XZ plane separates space into +y and -y side. In short, these Reference planes divide complete space into eight spaces or OCTANTS based on the +/-ve nature of x, y and z.
How do we take X, Y and Z axes in Cartesian Coordinate System?
The X, Y and Z axes forming a frame of reference for Cartesian Coordinate System, must be mutually perpendicular.
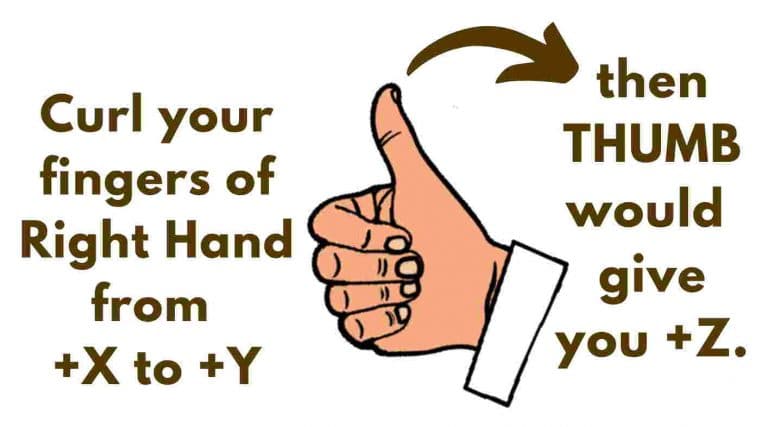
In addition to that these axes must taken according to Right Hand Thumb Rule.
Let’s say you have fixed X & Y axes as in figure (A). Now you won’t have a choice for Z axis. It must be perpendicular to both X & Y and direction must be inline with Right Hand Rule as shown in figure (C).
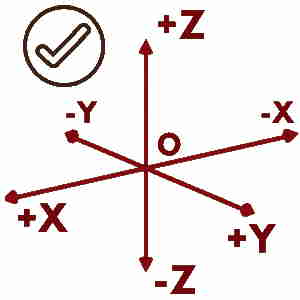
Interpretation of Cartesian Coordinates viz. x, y and z
Watch: How x, y and z coordinates are defined for Cartesian Coordinate System?
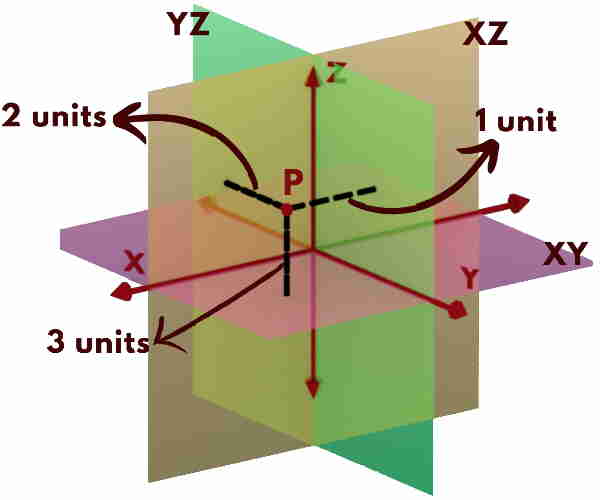
Assume that a point in space is P (1, 2, 3). That is, x-coordinate = 1; y-coordinate = 2; z-coordinate = 3.
x coordinate is 1 means, perpendicular distance of the point P from YZ plane is 1 unit.
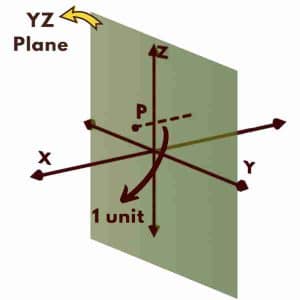
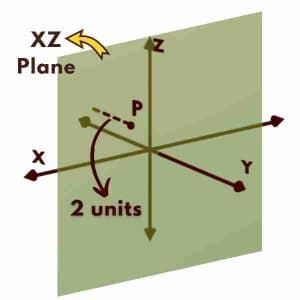
y coordinate is 2 means, perpendicular distance of the point P from XZ plane is 2 units.
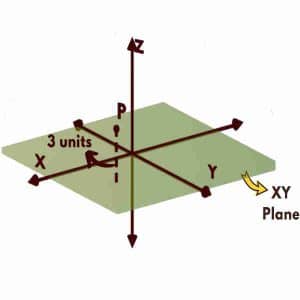
z coordinate is 3 means, perpendicular distance of the point P from XY plane is 3 units.
So point P (1, 2, 3) is uniquely represented in the space from the reference as: At a distance of 1 unit from YZ plane in +X side AND distance of 2 units from XZ plane in +Y side AND distance of 3 units from XY plane in +Z side
What if any coordinate is negative?
Let’s assume P (-1, 2, 3) i.e. x coordinate is negative.
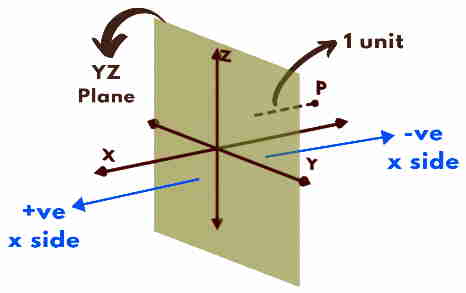
Point P is still at a perpendicular distance of 1 unit from the YZ plane; but present on the other side i.e. on the negative side of x. Like-wise for y & z coordinates.
Constant Coordinate Surfaces
What would be the locus if we are given with only one coordinate?
Assume that we are given with x = 3 while y and z coordinates can take any value. Then what would be the locus?
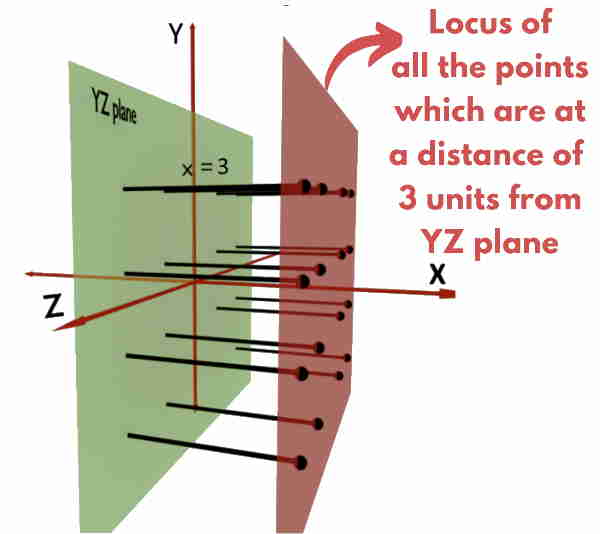
We are given with x coordinate equal to 3 i.e. x = constant and no restrictions over the values of y and z coordinates. So, just apply the definition of x coordinate. It is the perpendicular distance from YZ plane. And in this case we want locus of all such points which are at perpendicular distance of 3 units in positive direction from the YZ plane. as shown in the figure.
So locus of x = constant (any value) is a plane or surface parallel to YZ plane present at that x.
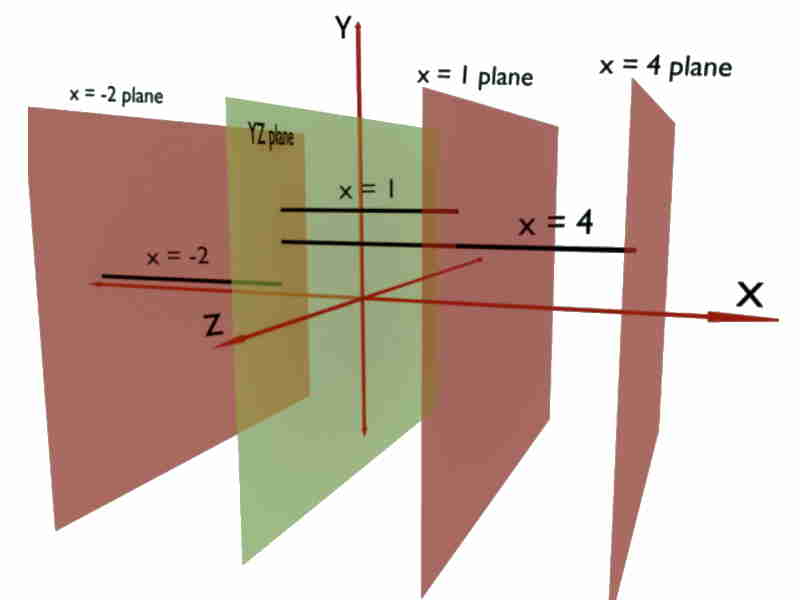
Similarly, locus of y = constant (any value) is a plane or surface parallel to XZ plane present at that ‘y’. And, locus of z = constant (any value) is a plane or surface parallel to XY plane present at that ‘z’.
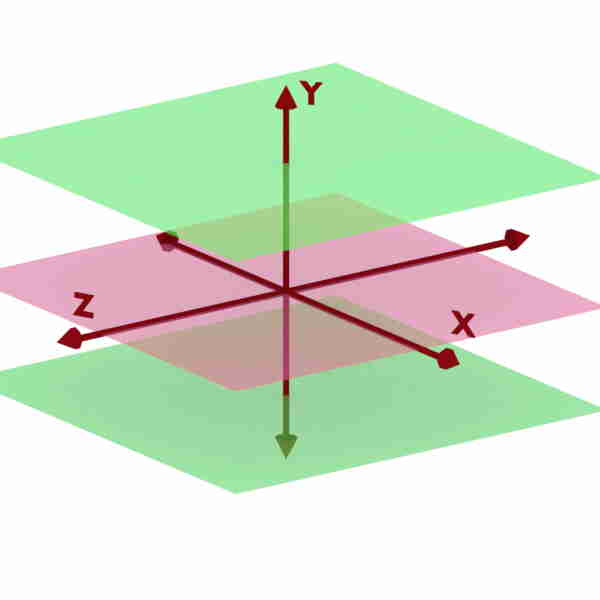
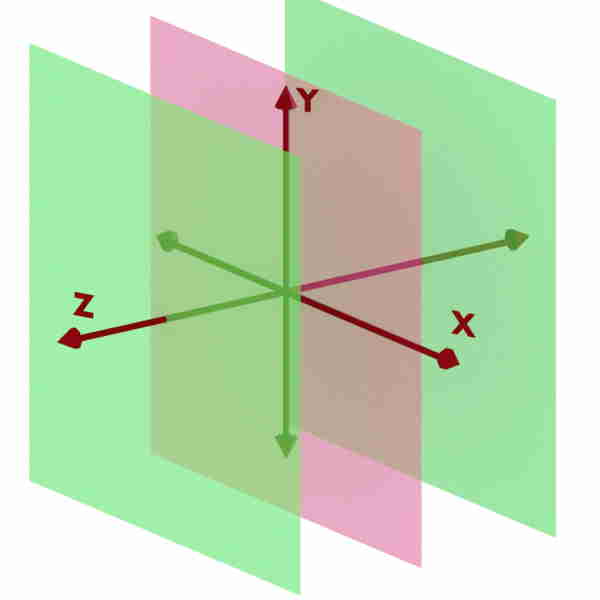
Can you locate y = 3; -1 < x < 1; -2 < z < 2 ?
We know that y = constant is a plane or surface parallel to XZ plane. So y = 3 will be plane parallel to XZ plane present at y = 3.
But here x and z coordinates are not completely “Don’t cares”. But we are given with their ranges. So the plane will not be infinite one but only extended up to the given range of x and z.
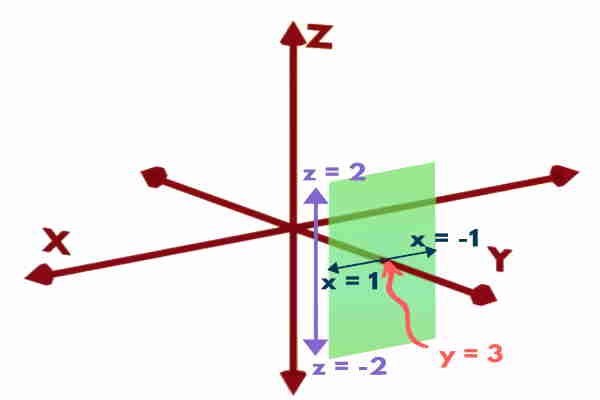
So, for constant coordinate surfaces:
- ONE Coordinate constant & other TWO are Variables then the locus is a Plane or Surface parallel to one of the Reference planes.
- OR Vice-versa: Equation of the Plane/Surface parallel to one of the reference planes is ONE coordinate Constant & others Variables.
- If the given equation of plane/surface is given as ONE Coordinate constant and Range for Other Variable Coordinates is mentioned; then Plane is Finite else take it as an infinite.
But, what would be the equation of a plane or surface which is not parallel to any of the reference planes?
These are expressed by functions and normally you deal them in Mathematics.
Constant Coordinates Lines
What would be locus if we are given with two coordinates constants & remaining one variable?
Simple! It would be a line parallel to one the reference axes corresponding to variable coordinate.
Let us find locus of x = -2 and y = 3.
We know that x = -2 will represent a plane parallel to YZ plane and present at x = -2. Similarly, y = 3 will represent a plane parallel to XZ plane and present at y = 3.
So our required locus will be the intersection of these two planes.
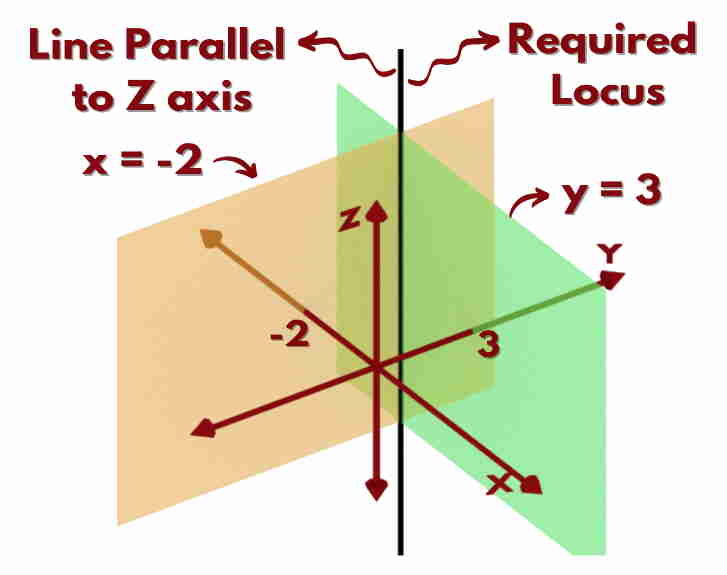
So, for constant Coordinates Lines:
- x and y coordinates constants while z variable, locus is a LINE parallel to Z axis.
- y and z coordinates constants while x variable, locus is a LINE parallel to X axis.
- x and z coordinates constants while y variable, locus is a LINE parallel to Y axis.
- Conversely, equation of a line parallel to one of the reference axis is TWO coordinates as constants and remaining ONE as variable.
- If range of variable coordinate is given then it would be finite line otherwise infinite.
What if all the coordinates are constants or given?
Let’s have, x = 1, y = 2 & z = 3.
The locus can be thought as an intersection of THREE planes viz. x =1 plane, y = 2 plane and z = 3 plane.
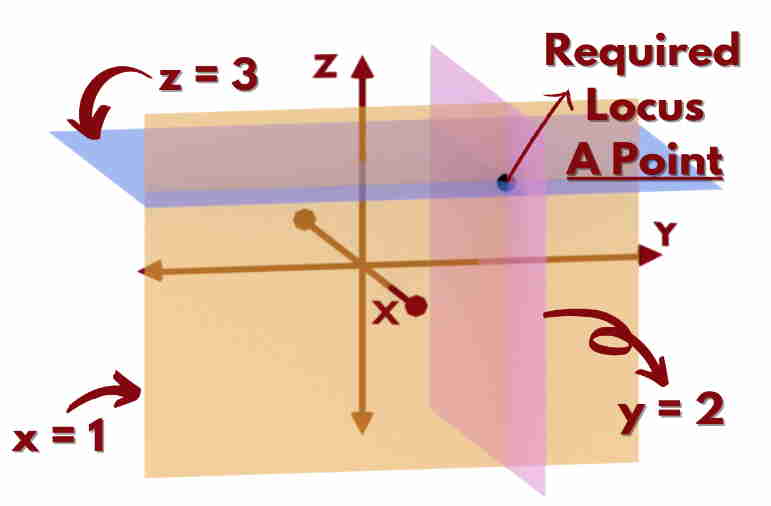
Why is Cartesian Coordinate System called as Rectangular Coordinate System?
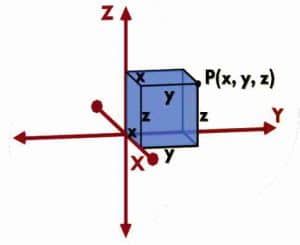
Simple! Doesn’t this look like a Rectangular box?
How vectors are represented in Cartesian System?
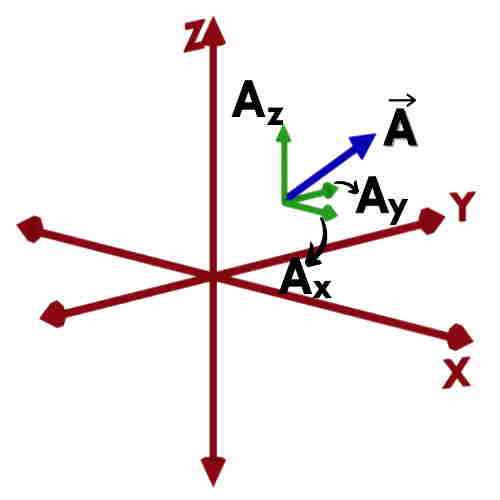
The general way of representation for the vectors is as follows:

Ax , Ay and Az are the X, Y and Z components of the vector while ax , ay and az are the unit vectors of Cartesian Coordinates.
What is a vector?
It is an entity having magnitude and direction represented by an arrow indicating the magnitude by its length and the direction by an arrow head.
Vectors are crucial for the study of Electromagnetics. Basically you can’t imagine EMT without vectors. Electric Field, Magnetic Field, EM Wave propagation, Waveguides, Antennas, everywhere, you need vectors.
What is a component of vector?
Basically, a vector represents the influence (magnitude + direction) of the entity pictorially.
So in Cartesian Coordinate System, think like this:
The total influence is broken into 3 influences viz. parallel to X, Y and Z axes.
So the influence or effect of the given vector parallel to X axis is the X-component of vector. Similarly its influence parallel to Y and Z axes are the Y-component & Z-component respectively.
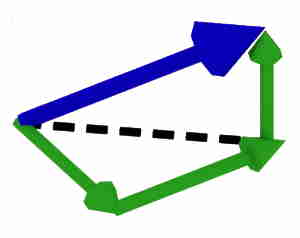
Actually, the vector addition of all the components results into the the original vector.
How are the Unit Vectors defined for a Cartesian Coordinate System?
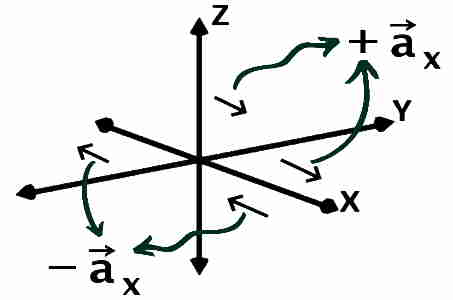
Unit vector {\overrightarrow a}_x or a is the vector of unit magnitude pointing in the increasing X direction while -{\overrightarrow a}_x is the vector of unit magnitude pointing in decreasing X direction.
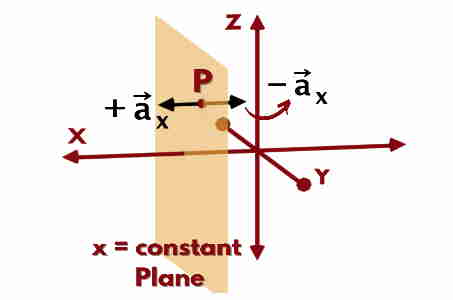
Actually, unit vector a at the given point P, is the vector of unit magnitude and normal (perpendicular) to x = constant plane ( | | to YZ) at that point P. The one, pointing to increasing X will be +ve & other will be -ve.
Similarly, unit vectors {\overrightarrow a}_y & {\overrightarrow a}_z at the given point P, are the vectors of unit magnitude and normal i.e. perpendicular to y = constant (|| to XZ)& z = constant (|| to XY) planes at that point P, respectively. The ones pointing to increasing direction will be positive & other one negative.
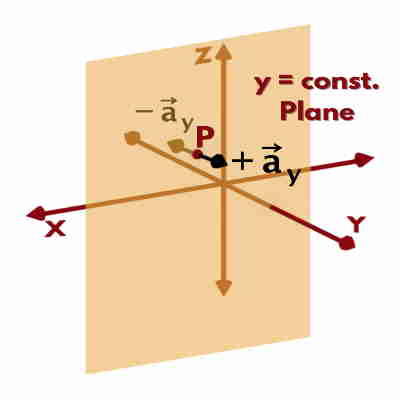
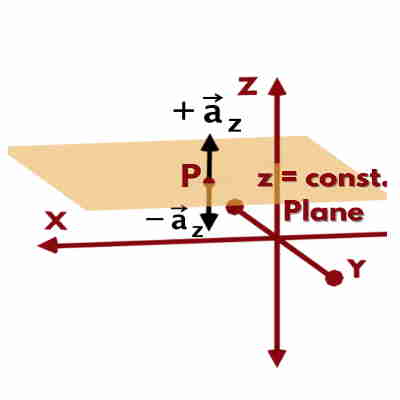
Any vector in Cartesian Coordinate System is represented using these unit vectors.
Say, a force of 10 N is acting along decreasing Y direction. So, this entity is represented by a vector of segment length 10 units with unit vector -{\overrightarrow a}_y .
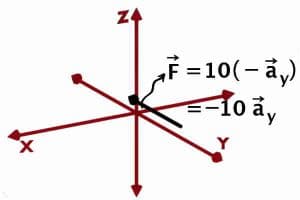
Do you Know? If the starting point is not explicitly given then you can draw that vector anywhere in the space preserving its influence viz. magnitude & direction.
Do not forget to check our Awesome GATE courses.


