Gate 2022 Question Paper with Answer Keys for Electronics and Comm. Engineering (EC)
Q.1 – Q.5 Carry ONE mark each.
Q.1 Mr. X speaks _______ Japanese ______ Chinese.
(A) neither / or
(B) either / nor
(C) neither / nor
(D) also / but
Ans. c) neither / nor
Q.2 A sum of money is to be distributed among P, Q, R, and S in the proportion 5 : 2 : 4 : 3, respectively. If R gets ₹ 1000 more than S, what is the share of Q (in ₹)?
(A) 500
(B) 1000
(C) 1500
(D) 2000
Ans. (D) 2000
Q.3 A trapezium has vertices marked as P, Q, R and S (in that order anticlockwise). The side PQ is parallel to side SR.Further, it is given that, PQ = 11 cm, QR = 4 cm, RS = 6 cm and SP = 3 cm. What is the shortest distance between PQ and SR (in cm)?
(A) 1.80
(B) 2.40
(C) 4.20
(D) 5.76
Ans. (B) 2.40
Q.4 The figure shows a grid formed by a collection of unit squares. The unshaded unit square in the grid represents a hole. What is the maximum number of squares without a “hole in the interior” that can be formed within the 4 × 4 grid using the unit squares as building blocks?
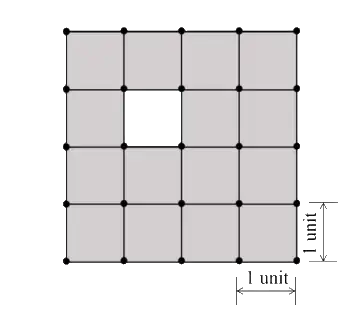
(A) 15
(B) 20
(C) 21
(D) 26
Ans. (B) 20
Q.5 An art gallery engages a security guard to ensure that the items displayed are protected. The diagram below represents the plan of the gallery where the
boundary walls are opaque. The location the security guard posted is identified such that all the inner space (shaded region in the plan) of the gallery is within
the line of sight of the security guard. If the security guard does not move around the posted location and has a 360oview, which one of the following correctly represents the set of ALL possible locations among the locations P, Q, R and S, where the security guard can be posted to watch over the entire inner space of the gallery.

(A) P and Q
(B) Q
(C) Q and S
(D) R and S
Ans. (C) Q and S
Q. 6 – Q. 10 Carry TWO marks each.
Q.6 Mosquitoes pose a threat to human health. Controlling mosquitoes using chemicals may have undesired consequences. In Florida, authorities have used
genetically modified mosquitoes to control the overall mosquito population. It remains to be seen if this novel approach has unforeseen consequences.
Which one of the following is the correct logical inference based on the information in the above passage?
(A) Using chemicals to kill mosquitoes is better than using genetically modified mosquitoes because genetic engineering is dangerous
(B) Using genetically modified mosquitoes is better than using chemicals to kill mosquitoes because they do not have any side effects
(C) Both using genetically modified mosquitoes and chemicals have undesired consequences and can be dangerous
(D) Using chemicals to kill mosquitoes may have undesired consequences but it is not clear if using genetically modified mosquitoes has any negative consequence
Ans. (C) Both using genetically modified mosquitoes and chemicals have undesired consequences and can be dangerous
Q.7 Consider the following inequalities.
(i) 2x − 1 > 7
(ii) 2x − 9 < 1
Which one of the following expressions below satisfies the above two inequalities?
(A) x ≤ −4
(B) −4 < x ≤ 4
(C) 4 < x < 5
(D) x ≥ 5
Ans. (C) 4 < x < 5
Q.8 Four points P(0, 1), Q(0, −3), R(−2, −1), and S(2, −1) represent the vertices of a quadrilateral. What is the area enclosed by the quadrilateral?
(A) 4
(B) 4 \sqrt{2}
(C) 8
(D) 8 \sqrt{2}
Ans. (C) 8
Q.9 In a class of five students P, Q, R, S and T, only one student is known to have copied in the exam. The disciplinary committee has investigated the situation
and recorded the statements from the students as given below.
Statement of P: R has copied in the exam.
Statement of Q: S has copied in the exam.
Statement of R: P did not copy in the exam.
Statement of S: Only one of us is telling the truth.
Statement of T: R is telling the truth.
The investigating team had authentic information that S never lies. Based on the information given above, the person who has copied in the exam is
(A) R
(B) P
(C) Q
(D) T
Ans. (B) P
Q.10 Consider the following square with the four corners and the center marked as P, Q, R, S and T respectively. Let X, Y and Z represent the following operations:
X: rotation of the square by 180 degree with respect to the S-Q axis.
Y: rotation of the square by 180 degree with respect to the P-R axis.
Z: rotation of the square by 90 degree clockwise with respect to the axis perpendicular, going into the screen and passing through the point T.
Consider the following three distinct sequences of operation (which are applied in the left to right order).
(1) XYZZ
(2) XY
(3) ZZZZ
Which one of the following statements is correct as per the information provided above?
(A) The sequence of operations (1) and (2) are equivalent
(B) The sequence of operations (1) and (3) are equivalent
(C) The sequence of operations (2) and (3) are equivalent
(D) The sequence of operations (1), (2) and (3) are equivalent
Ans. (B) The sequence of operations (1) and (3) are equivalent
Q.11 – Q.35 Carry ONE mark Each
Q.11 Consider the two-dimensional vector field \overrightarrow{F}(x,y)=x\overrightarrow{i}+y\overrightarrow{j} denote the unit vectors along the x-axis and the y-axis, respectively. A contour C in the x-y plane, as shown in the figure, is composed of two horizontal lines connected at the two ends by two semicircular arcs of unit radius. The contour is traversed in the counter-clockwise sense. The value of the closed path integral \oint _{c}\overrightarrow{F}(x,y)\cdot (dx\overrightarrow{i}+dy \overrightarrow{j}) is _______.
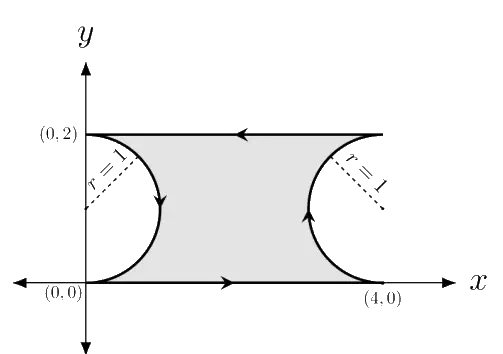
(A) 0
(B) 1
(C) 8 + 2 \pi
(D) −1
Ans. (A) 0
Q.12. Consider a system of linear equations Ax=b where
A=\begin{bmatrix}1 & -\sqrt{2} & 3\\-1 & \sqrt{2} & -3\end{bmatrix},b=\begin{bmatrix}1\\3\end{bmatrix}This system of equations admits ______.
(A) a unique solution for x
(B) infinitely many solutions for x
(C) no solutions for x
(D) exactly two solutions for x
Ans. (C) no solution for x
Q.13 The current I in the circuit shown is ____.
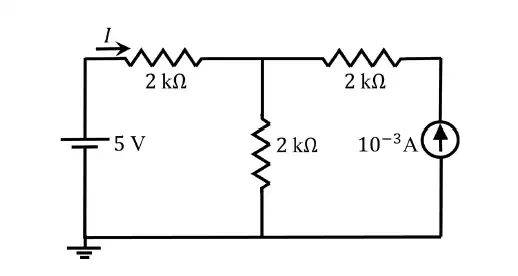
(A) 1.25 × 10-3A
(B) 0.75 × 10-3A
(C) −0.5 × 10-3A
(D) 1.16 × 10-3A
Ans. (B) 0.75 x 10-3 A
Q.14 Consider the circuit shown in the figure. The current I flowing through the 10 Ω resistor is _______.
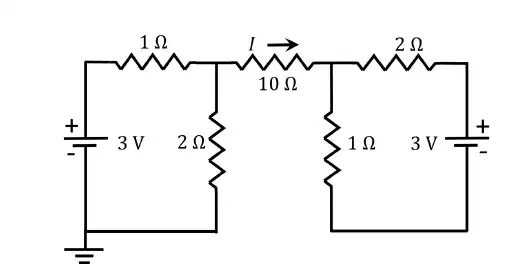
(A) 1 A
(B) 0 A
(C) 0.1 A
(D) -0.1 A
Ans.(B) 0 A
Q.15 The Fourier transform x(j \omega ) of the signal x(t)=\frac{t}{(1+t^{2})^{2}} is ___.
(A) \frac{\pi }{2j}\omega e^{-|\omega |}
(B) \frac{\pi }{2}\omega e^{-|\omega |}
(C) \frac{\pi }{2j} e^{-|\omega |}
(D) \frac{\pi }{2} e^{-|\omega |}
Ans. (A) \frac{\pi }{2j}\omega e^{-|\omega |}
Q.16. Consider a long rectangular bar of direct bandgap p-type semiconductor. The equilibrium hole density is 1017 cm-3 and the intrinsic carrier concentration is 1010 cm-3. Electron and hole diffusion lengths are 2 \mu m and 1 \mum, respectively. The left side of the bar (x= 0) is uniformly illuminated with a laser having photon energy greater than the bandgap of the semiconductor. Excess electron-hole pairs are generated ONLY at x = 0 because of the laser. The steady state electron density at x= 0 is 1014 cm-3 due to laser illumination. Under these conditions and ignoring electric field, the closest approximation (among the given options) of the steady state electron density at x = 2 \mu m, is _ .
(A) 0.37 × 1014 cm-3
(B) 0.63 × 1013 cm-3
(C) 3.7 × 1014 cm-3
(D) 103 cm-3
Ans. (A) 0.37 × 1014 cm-3
Q.17 In a non-degenerate bulk semiconductor with electron density n= 1016cm-3, the value of Ec-EFn = 200 meV, where Ec and EFn denote the bottom of the conduction band energy and electron Fermi level energy, respectively. Assume thermal voltage as 26 meV and the intrinsic carrier concentration is 1010 cm-3. For n = 0.5 × 1016 cm-3, the closest approximation of the value of (Ec − EFn), among the given options, is ___.
(A) 226 meV
(B) 174 meV
(C) 218 meV
(D) 182 meV
Ans. (C) 218 meV
Q.18 Consider the CMOS circuit shown in the figure (substrates are connected to their respective sources). The gate width (W) to gate length (L) ratios (W/L) of the transistors are as shown. Both the transistors have the same gate oxide capacitance per unit area. For the pMOSFET, the threshold voltage is -1 V and the mobility of holes is 40 cm2 /V.s . For the nMOSFET, the threshold voltage is 1 V and the mobility of electrons is 300 cm2/ V.s . The steady state output voltage Vo is ___.
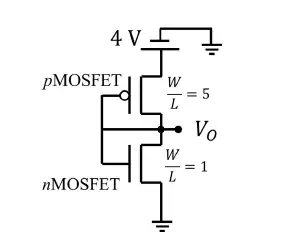
(A) equal to 0 V
(B) more than 2 V
(C) less than 2 V
(D) equal to 2 V
Ans. (C) less than 2 V
Q.19 Consider the 2-bit multiplexer (MUX) shown in the figure. For OUTPUT to be the XOR of C and D, the values for A0, A1, A2, and A3 are __.
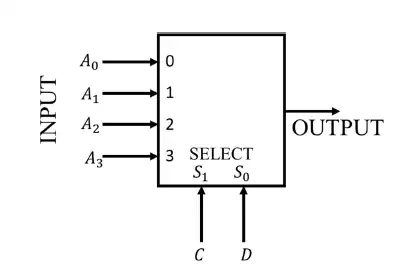
(A) A0 = 0, A1 = 0, A2 = 1, A3 = 1
(B) A0 = 1, A1 = 0, A2 = 1, A3 = 0
(C) A0 = 0, A1 = 1, A2 = 1, A3 = 0
(D) A0 = 1, A1 = 1, A2 = 0, A3= 0
Ans. (C) A0 = 0, A1 = 1, A2 = 1, A3 = 0
Q.20 The ideal long channel nMOSFET and pMOSFET devices shown in the circuits have threshold voltages of 1 V and −1 V, respectively. The MOSFET substrates are
connected to their respective sources. Ignore leakage currents and assume that the capacitors are initially discharged. For the applied voltages as shown, the steady state voltages are _____.
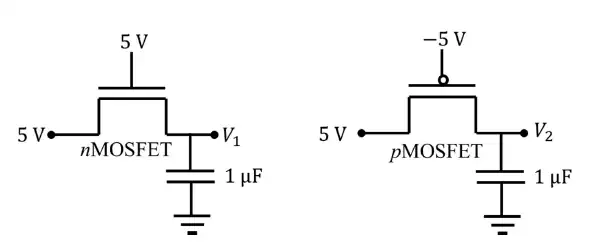
(A) V1 = 5 V, V2 = 5 V
(B) V1 = 5 V, V2= 4 V
(C)V1 = 4 V, V2= 5 V
(D) V1 = 4 V, V2 = −5 V
Ans. (C) V1 = 4 V, V2= 5 V
Q.21 Consider a closed-loop control system with unity negative feedback and KG(s) in the forward path, where the gain K= 2. The complete Nyquist plot of the transfer function G(s) is shown in the figure. Note that the Nyquist contour has been chosen to have the clockwise sense. Assume G(s) has no poles on the closed right-half of the complex plane. The number of poles of the closed-loop transfer function in the closed right-half of the complex plane is _____. .
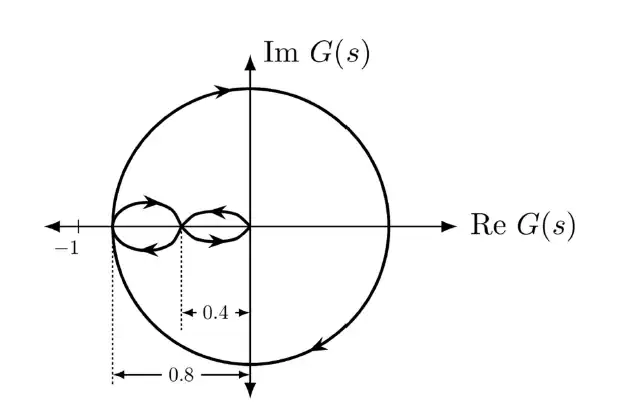
(A) 0
(B) 1
(C) 2
(D) 3
Ans. (C) 2
Q.22 The root-locus plot of a closed-loop system with unity negative feedback and transfer function KG(s) in the forward path is shown in the figure. Note that K is varied from 0 to ∞. Select the transfer function G(s) that results in the root-locus plot of the closed-loop system as shown in the figure.
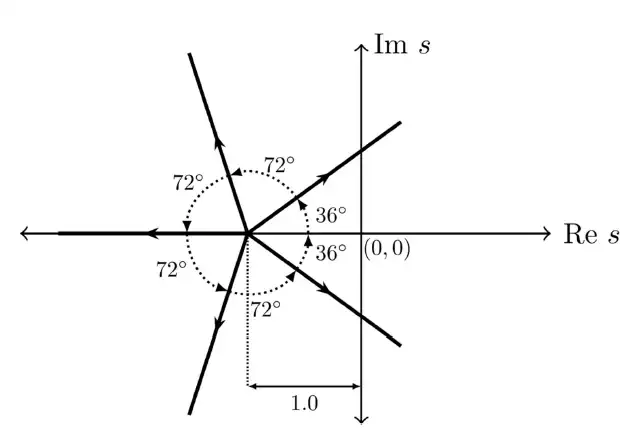
(A) G(s)=\frac{1}{(s+1)^{5}}
(B) G(s)=\frac{1}{s^5+1}
(C) G(s)=\frac{s-1}{(s+1)^{6}}
(D) G(s)=\frac{s+1}{s^6+1^{5}}
Ans. (A) G(s)=\frac{1}{(s+1)^{5}}
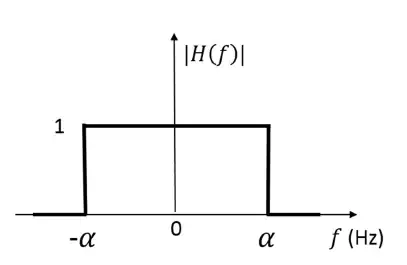
Q.23 The frequency response H(f) of a linear time-invariant system has magnitude as shown in the figure.
Statement I: The system is necessarily a pure delay system for inputs which are bandlimited to − \alpha ≤ f ≤ \alpha .
Statement II: For any wide-sense stationary input process with power spectral density SX(f), the output power spectral density SY(f) obeys SY(f) = SX(f) for −α ≤ f ≤ α. Which one of the following combinations is true?
Statement I is correct, Statement II is correct
(B) Statement I is correct, Statement II is incorrect
(C) Statement I is incorrect, Statement II is correct
(D) Statement I is incorrect, Statement II is incorrect
Ans. (C) Statement I is incorrect, Statement II is correct
Q.24In a circuit, there is a series connection of an ideal resistor and an ideal capacitor. The conduction current (in Amperes) through the resistor is 2sin(t + \pi /2).
The displacement current (in Amperes) through the capacitor is _____
(A) 2sin(t)
(B) 2sin(t + \pi )
(C) 2sin(t + \pi /2)
(D) 0
Ans. (C) 2sin(t + \pi /2)
Q.25 Consider the following partial differential equation (PDE)
a\frac{\partial ^{2}f(x,y)}{\partial x^{2}}+b\frac{\partial ^{2}f(x,y)}{\partial y^{2}}=f(x,y) where a and b are distinct positive real numbers. Select the combination(s) of values of the real parameters ξ and \eta such that f(x,y)=e^{(\xi x+y)} is a solution of the given PDE.
(A) \xi =\frac{1}{\sqrt{2a}},\eta =\frac{1}{\sqrt{2b}}
(B) \xi =\frac{1}{\sqrt{a}},\eta =0
(C) \xi =0,\eta =0
(D) \xi =\frac{1}{\sqrt{a}},\eta = \frac{1}{\sqrt{b}}
Ans. (A) or (B)
Q.26 An ideal OPAMP circuit with a sinusoidal input is shown in the figure. The 3 dB frequency is the frequency at which the magnitude of the voltage gain decreases by 3 dB from the maximum value. Which of the options is/are correct?
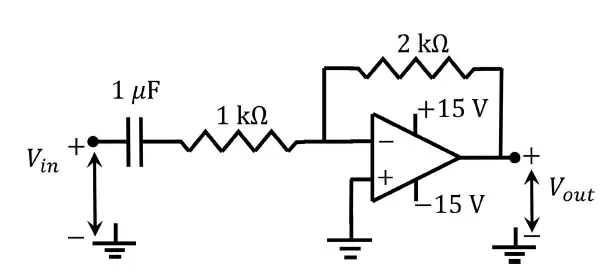
(A) The circuit is a low pass filter.
(B) The circuit is a high pass filter.
(C) The 3 dB frequency is 1000 rad/s.
(D) The 3 dB frequency is 1000/3 rad/s
Ans. (B),(C)
Q.27 Select the Boolean function(s) equivalent to x+yz, where x,y, and z are Boolean variables, and + denotes logical OR operation.
(A) x+z+xy
(B) (x+y)(x+z)
(C) x+xy+yz
(D) x+xz+xy
Ans.(B),(C)
Q.28 Select the correct statement(s) regarding CMOS implementation of NOT gates.
(A) Noise Margin High (NMH) is always equal to the Noise Margin Low (NML ), irrespective of the sizing of transistors.
(B) Dynamic power consumption during switching is zero.
(C) For a logical high input under steady state, the nMOSFET is in the linear regime of operation.
(D) Mobility of electrons never influences the switching speed of the NOT gate.
Ans. (C) For a logical high input under steady state, the nMOSFET is in the linear regime of operation.
Q.29Let H(X) denote the entropy of a discrete random variable X taking K possible distinct real values. Which of the following statements is/are necessarily true?
(A) H(X) ≤ log2 K bits
(B)H(X) ≤ H(2X)
(C) H(X) ≤ H(X2)
(D) H(X) ≤ H(2X )
Ans. (A),(B),(D)
Q.30 Consider the following wave equation,
\frac{\partial ^{2}f(x,t)}{\partial t^{2}}=1000 \frac{\partial ^{2}f(x,t)}{\partial x^{2}}
Which of the given options is/are solution(s) to the given wave equation?
(A) f(x,t)=e^{-(x-100t)^{2}}+e^{-(x+100t)^{2}}
(B) f(x,t)=e^{-(x-100t)}+0.5 e^{-(x+100t)}
(C) f(x,t)= e^{-x-100t}+sin(x+100t)
(D) f(x,t)=e^{j100\pi (-100x+t)}+e^{j100\pi (100x+t)}
Ans. (A), (C)
Q.31 The bar graph shows the frequency of the number of wickets taken in a match by a bowler in her career. For example, in 17 of her matches, the bowler has taken 5 wickets each. The median number of wickets taken by the bowler in a match is __ (rounded off to one decimal place).
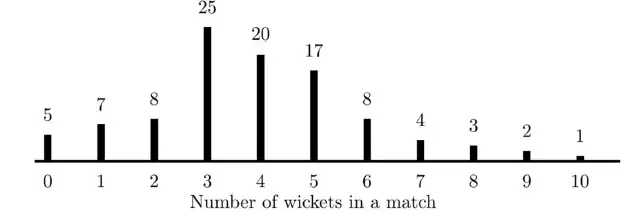
Ans. 4.0 to 4.0
Q.32 A simple closed path C in the complex plane is shown in the figure. If
\oint _{C}\frac{2^{z}}{z^{2}-1}dz=-i\pi A where i= \sqrt{-1} , then the value of A is ____. (rounded off to two decimal places)
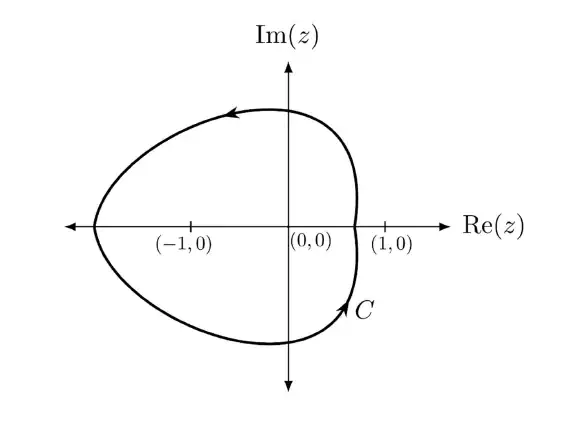
Ans.0.50 to 0.50
Q.33 Let x1(t)=e-tu(t) and x2(t) = u(t)-u(t-2) , where u(.) denotes the unit step function.
If u(.) denotes the convolution of x1(t) and x2(t) , then lim_{t\rightarrow \infty }y(t) (rounded off to one decimal place).
Ans.0.0 to 0.0
Q.34 An ideal MOS capacitor (p-type semiconductor) is shown in the figure. The MOS capacitor is under strong inversion with VG = 2 V. The corresponding inversion charge density (QIN) is 2.2 \mu C/cm2. Assume oxide capacitance per unit area as COX = 1.7 \mu F/cm2. For VG = 4 V, the value of QIN is __ \mu C/cm2 (rounded off to one decimal place).
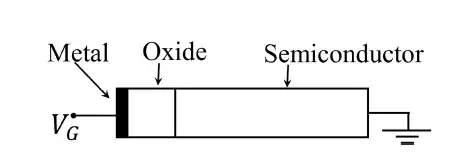
Ans. 5.5 to 5.7
Q.35 A symbol stream contains alternate QPSK and 16-QAM symbols. If symbols from this stream are transmitted at the rate of 1 mega-symbols per second, the raw (uncoded) data rate is _ mega-bits per second (rounded off to one decimal place).
Ans. 2.99 to 3.01
Q.36 The function f(x) = 8 loge x -x2 + 3 attains its minimum over the interval [1, e] at x = _____.
(Here logex is the natural logarithm of x.)
(A) 2
(B) 1
(C) e
(D) \frac{1+e}{2}
Ans. (B) 1
Q.37 Let α, β be two non-zero real numbers and v1, v2 be two non-zero real vectors of size 3 × 1. Suppose that v1 and v2 satisfy v1Tv2 = 0 , v1Tv1 = 1 and v2Tv2=1. Let A be the 3×3 matrix given by, A=αv1v1T + βv2v2T . The eigen values of A are ______. .
(A) 0, α , β
(B) 0, α + β, α − β
(C) 0, \frac{\alpha +\beta }{2},\sqrt{\alpha \beta } ,
(D) 0,0, \sqrt{\alpha^{2} + \beta^{2} }
Ans. (A) 0, α, β
Q.38 For the circuit shown, the locus of the impedance Z(jω) is plotted as ω increases from zero to infinity. The values of R1 and R2 are:
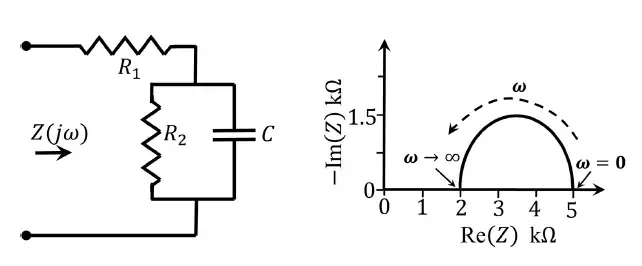
(A) R1 = 2 kΩ, R2 = 3 kΩ
(B) R1 = 5 kΩ, R2 = 2 kΩ
(C) R1= 5 kΩ, R2 = 2.5 kΩ
(D) R1 = 2 kΩ, R2 = 5 kΩ
Ans. (A) R1 = 2 kΩ, R2 = 3 kΩ
Q.39 Consider the circuit shown in the figure with input V(t) in volts. The sinusoidal steady state current I(t) flowing through the circuit is shown graphically (where t is in seconds). The circuit element Z can be ____
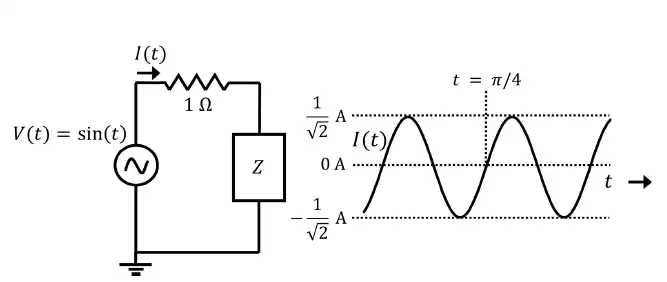
(A) a capacitor of 1 F
(B) an inductor of 1 H
(C) a capacitor of \sqrt{3} F
(D) an inductor of \sqrt{3} H
Ans. (B) an inductor of 1 H
Q.40 Consider an ideal long channel nMOSFET (enhancement-mode) with gate length 10 μm and width 100 μm. The product of electron mobility (μn ) and oxide
capacitance per unit area (Cox ) is μn Cox = 1 mA/V2. The threshold voltage of the transistor is 1 V. For a gate-to-source voltage VGS = [2 − sin(2t)] V and drain-to source voltage VDS = 1 V (substrate connected to the source), the maximum value of the drain-to-source current is ___.
(A) 40 mA
(B) 20 mA
(C) 15 mA
(D) 5 mA
Ans. (C) 15 mA
Q.41 For the following circuit with an ideal OPAMP, the difference between the maximum and the minimum values of the capacitor voltage (Vc) is __.
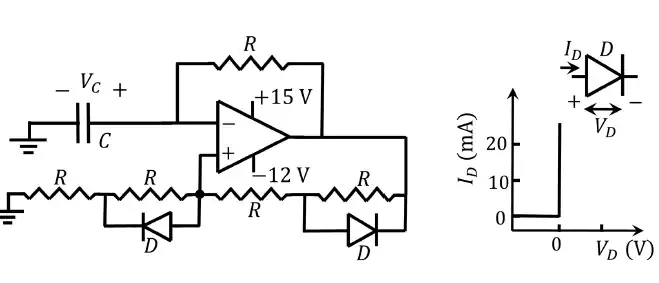
(A) 15 V
(B) 27 V
(C) 13 V
(D) 14 V
Ans. (C) 13 V
Q.42 A circuit with an ideal OPAMP is shown. The Bode plot for the magnitude (in dB) of the gain transfer function (AV(jω) = Vout(jω)/Vin(jω)of the circuit is also provided (here, ω is the angular frequency in rad/s). The values of R and C are __.
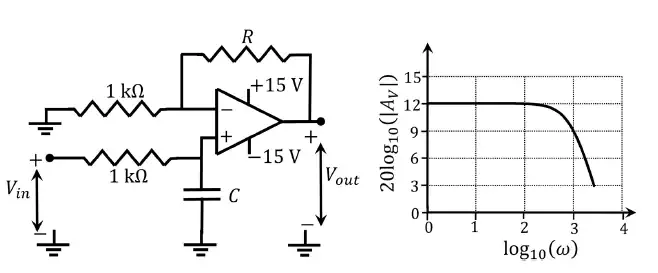
(A) R= 3 kΩ, C = 1 \mu F
(B) R = 1 kΩ, C = 3 \muF
(C) R = 4 kΩ, C = 1 \muF
(D) R= 3 kΩ, C = 2 \muF
Ans. (A) R= 3 kΩ, C = 1 \mu F
Q.43 For the circuit shown, the clock frequency is fo and the duty cycle is 25%. For the signal at the Q output of the Flip-Flop, _____.
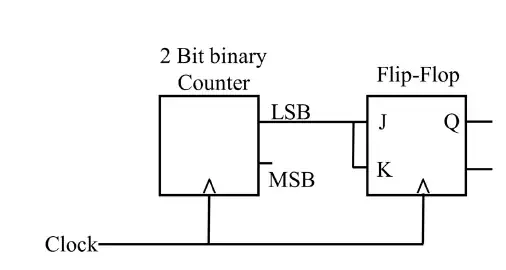
(A) frequency is fo/4 and duty cycle is 50%
(B) frequency is fo/4 and duty cycle is 25%
(C) frequency is fo/2 and duty cycle is 50%
(D) frequency is fo and duty cycle is 25%
Ans. (A) frequency is fo/4 and duty cycle is 50%
Q.44 Consider an even polynomial p(s) given by p(s) = s4 + 5s2 + 4 + K ,
where K is an unknown real parameter. The complete range of K for which p(s) has all its roots on the imaginary axis is _.
(A) −4 ≤ K ≤ 9/4
(B) −3 ≤ K ≤ 9/2
(C) −6 ≤ K ≤ 5/4
(D) −5 ≤ K ≤ 0
Ans. (A) −4 ≤ K ≤ 9/4
Q.45 Consider the following series:
\sum_{n=1}^{\infty }\frac{n^{d}}{c^{n}}
For which of the following combinations of c,d values does this series converge?
(A) c= 1, d = −1
(B) c= 2, d = 1
(C) c = 0.5, d= −10
(D) c = 1, d= −2
Ans. (B),(D)
Q.46 The outputs of four systems (S1, S2, S3, and S4) corresponding to the input signal sin(t), for all time t, are shown in the figure. Based on the given information, which of the four systems is/are definitely NOT LTI (linear and time-invariant)?
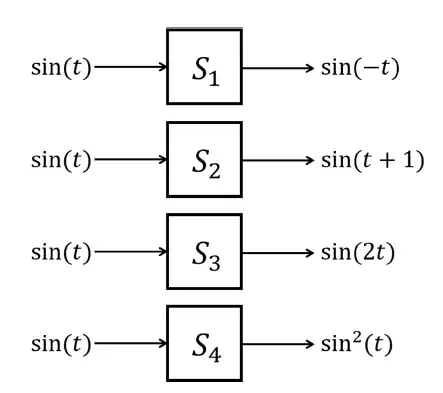
(A) S1
(B) S2
(C) S3
(D) S4
Ans. (C),(D)
Q.47 Select the CORRECT statement(s) regarding semiconductor devices.
(A) Electrons and holes are of equal density in an intrinsic semiconductor at equilibrium.
(B) Collector region is generally more heavily doped than Base region in a BJT.
(C) Total current is spatially constant in a two terminal electronic device in dark under steady state condition.
(D) Mobility of electrons always increases with temperature in Silicon beyond 300 K.
Ans. (A),(C)
Q.48 A state transition diagram with states A,B, and C, and transition probabilities p1, p2, … , p7 is shown in the figure (e.g., p1 denotes the probability of transition from state A to B). For this state diagram, select the statement(s) which is/are universally true.
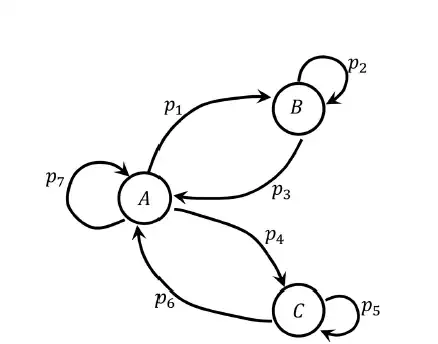
(A) p2+p3 = p5+p6
(B) p1+p3= p4 + p6
(C) p1 + p4 + p7 = 1
(D) p2 + p5 + p7 = 1
Ans. (A),(C)
Q.49 Consider a Boolean gate (D) where the output Y is related to the inputs A and B as, Y=A+\bar{B} , where + denotes logical OR operation. The Boolean inputs ‘0’ and ‘1’ are also available separately. Using instances of only D gates and inputs ‘0’ and ‘1’, __ (select the correct option(s)).
(A) NAND logic can be implemented
(B) OR logic cannot be implemented
(C) NOR logic can be implemented
(D) AND logic cannot be implemented
Ans. (A),(C)
Q.50 Two linear time-invariant systems with transfer functions
G_{1}(s)=\frac{10}{s^{2}+s+1} and G_{2}(s)=\frac{10}{s^{2}+s\sqrt{10}+10} have unit step responses y1(t) and y2(t) respectively. Which of the following statements is/are true?
(A) y1(t) and y2(t) have the same percentage peak overshoot.
(B) y1(t) and y2(t) have the same steady-state value.
(C) y1(t) and y2(t) have the same damped frequency of oscillation.
(D) y1(t) and y2(t) have the same 2% settling time.
Ans. (A) y1(t) and y2(t) have the same percentage peak overshoot.
Q.51 Consider an FM broadcast that employs the pre-emphasis filter with frequency response
H_pe(\omega )=1+\frac{j\omega }{\omega _{o}}
where \omega_o = 104 rad/sec.
For the network shown in the figure to act as a corresponding de-emphasis filter, the appropriate pair(s) of (R, C) values is/are ____..
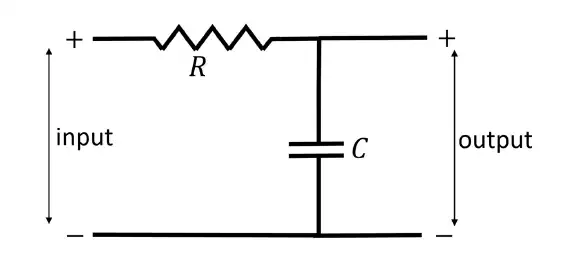
(A) R = 1 kΩ, C = 0.1 \muF
(B) R = 2 kΩ, C = 1 \muF
(C) R = 1 kΩ, C = 2 \muF
(D) R = 2 kΩ, C = 0.5 \muF
Ans. (A) R = 1 kΩ, C = 0.1 \muF
Q.52 A waveguide consists of two infinite parallel plates (perfect conductors) at a separation of 10-4 cm, with air as the dielectric. Assume the speed of light in air to be 3 × 108 m/s. The frequency/frequencies of TM waves which can propagate in this waveguide is/are
(A) 6 × 1015 Hz
(B) 0.5 × 1012 Hz
(C) 8 × 1014 Hz
(D) 1 × 1013 Hz
Ans. MTA
Q.53. The value of the integral \int \int_{D} 3(x^{2}+y^{2})dxdy
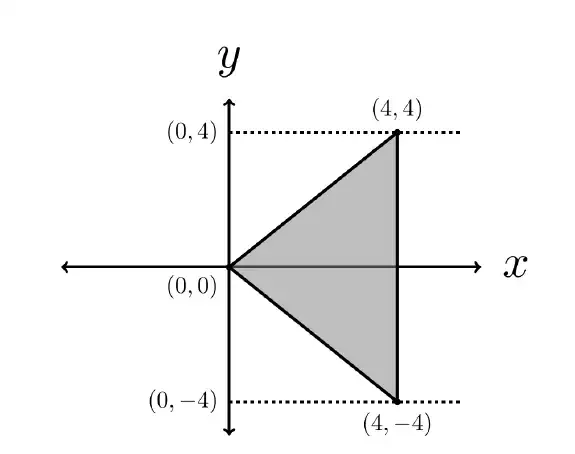
where D is the shaded triangular region shown in the diagram, is _ (rounded off to the nearest integer).
Ans. 512 to 512
Q.54 A linear 2-port network is shown in Fig. (a). An ideal DC voltage source of 10 V is connected across Port 1. A variable resistance R is connected across Port 2. As R is varied, the measured voltage and current at Port 2 is shown in Fig. (b) as a V2 versus −I2 plot. Note that for V2 = 5 V, I2 = 0 mA, and for V2 = 4 V, I2 = −4 mA.
When the variable resistance Rat Port 2 is replaced by the load shown in Fig. (c), the current I2 is ____ mA (rounded off to one decimal place) .
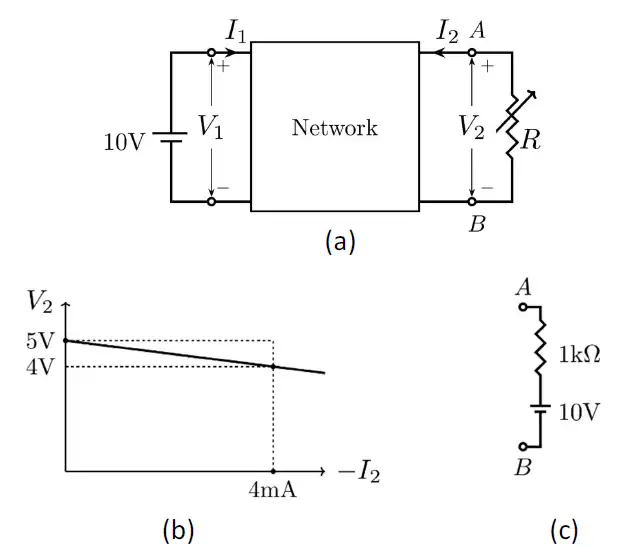
Ans. 3.9 to 4.1
Q.55. For a vector \bar{x}=[x[0],x[1],…..x[7] ] , the 8-point discrete Fourier transform (DFT) is denoted by \bar{X}=DFT\bar{x}=[x[0],x[1],…..x[7] ] where, X[k]=\sum_{n=0}^{7}x[n]exp\left ( -j\frac{2\pi }{8}nk \right ) Here, j= \sqrt{-1} . If \bar{X} = [1,0,0,0,2,0,0,0] and \bar{y} = DFT(DFT (\bar(x)) , then the value of y[0] is ____. (rounded off to one decimal place).
Ans. 7.9 to 8.1
Q.56 A p-type semiconductor with zero electric field is under illumination (low level injection) in steady state condition. Excess minority carrier density is zero at x = ±2ln , where ln = 10-4 cm is the diffusion length of electrons. Assume electronic charge, q = −1.6 × 10-19 C. The profiles of photo-generation rate of carriers and the recombination rate of excess minority carriers (R) are shown. Under these conditions, the magnitude of the current density due to the photo-generated electrons at x= +2ln is ______ mA/cm2 (rounded off to two decimal places).
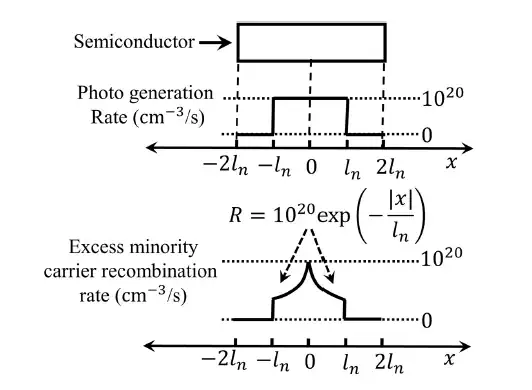
Ans. 0.57 to 0.61
Q.57 A circuit and the characteristics of the diode (D) in it are shown. The ratio of the minimum to the maximum small signal voltage gain \frac{\partial V_{out}}{\partial V_{in}} is ____- (rounded off to two decimal places).
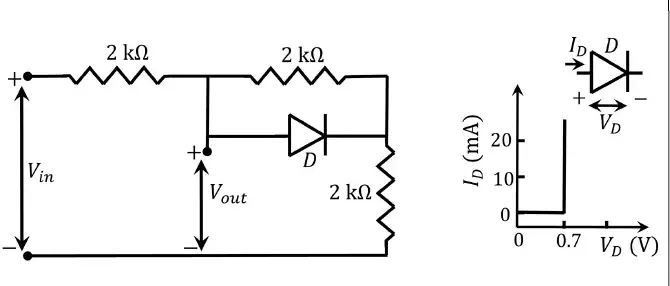
Ans.
Q.58 Consider the circuit shown with an ideal OPAMP. The output voltage Vo is __________V (rounded off to two decimal places).
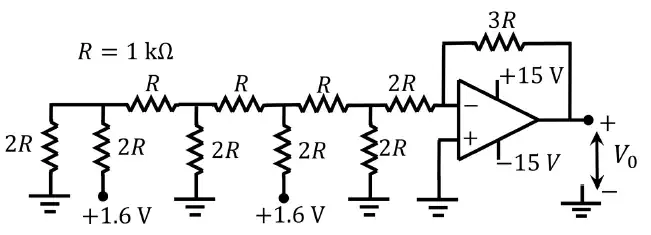
Ans. -0.55 to -0.45
Q.59. Consider the circuit shown with an ideal long channel nMOSFET (enhancementmode, substrate is connected to the source). The transistor is appropriately biased in the saturation region with VGG and VDD such that it acts as a linear amplifier. vi is the small-signal ac input voltage. vA and vB represent the small-signal voltages at the nodes A and B, respectively. The value of VA/VB is _____ (rounded off to one decimal place).
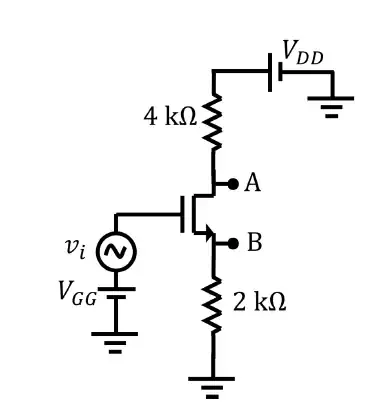
Ans. -2.1 to -1.9
Q.60. The block diagram of a closed-loop control system is shown in the figure. R(S), Y(S), and D(S) are the Laplace transforms of the time-domain signals r(t), y(t), and d(t), respectively. Let the error signal be defined as e(t) = r(t) − y(t). Assuming the reference input r(t) = 0 for all t, the steady-state error e(∞), due to a unit step disturbance d(t), is ____ (rounded off to two decimal places).
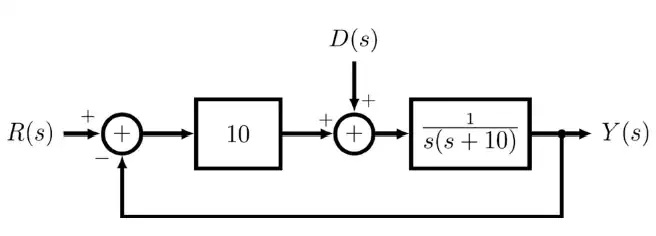
Ans. -0.11 to -0.09
Q.61 The transition diagram of a discrete memoryless channel with three input symbols and three output symbols is shown in the figure. The transition probabilities are as marked. The parameter \alpha lies in the interval [0.25, 1]. The value of α for which the capacity of this channel is maximized, is __ (rounded off to two decimal places).
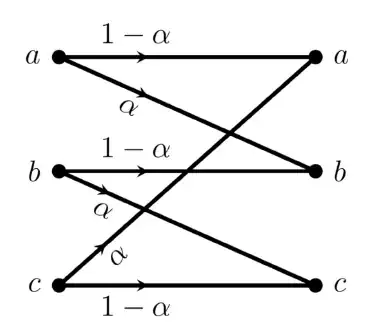
Ans. 1.00 to 1.00
Q.62 Consider communication over a memoryless binary symmetric channel using a (7, 4) Hamming code. Each transmitted bit is received correctly with probability (1 −ε ), and flipped with probability ε. For each codeword transmission, the receiver performs minimum Hamming distance decoding, and correctly decodes the message bits if and only if the channel introduces at most one bit error. For ε = 0.1, the probability that a transmitted codeword is decoded correctly is ______ (rounded off to two decimal places).
Ans. 0.84 to 0.86
Q.63 Consider a channel over which either symbol XA or symbol XB is transmitted. Let the output of the channel \delta be the input to a maximum likelihood (ML) detector at the receiver. The conditional probability density functions for \delta given XA and XB are:
f Y|xA (y) = e-(y+1) u(y+1),
f Y|xB (y) = e(y-1) (1-u(y-1)
where u(⋅) is the standard unit step function. The probability of symbol error for this system is _ (rounded off to two decimal places).
Ans. 0.22 to 0.25
Q.64. Consider a real valued source whose samples are independent and identically distributed random variables with the probability density function, f(x), as shown in the figure.
Consider a 1 bit quantizer that maps positive samples to value and others to value α. If α∗ and β∗ are the respective choices for α and β that minimize the mean square quantization error, then (α∗ − β∗) = ______ (rounded off to two decimal places).
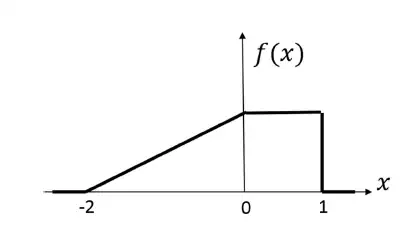
Ans. 1.15 to 1.18
Q.65 In an electrostatic field, the electric displacement density vector, \vec{D} is given by \vec{D}(x,y,z)=(x^{3}\vec{i}+y^{3}\vec{j}+xy^{2}\vec{k})
where \vec{i}, \vec{j}, \vec{k} are the unit vectors along x-axis, y-axis, and z-axis, respectively.
Consider a cubical region R centered at the origin with each side of length 1 m, and vertices at (±0.5 m, ±0.5 m, ±0.5 m). The electric charge enclosed within R is _____ C (rounded off to two decimal places).
Ans. 0.48 to 0.52
