Basics [Coordinate Systems/Vector Calculus]

Q.1 An electrostatic potential is given by \theta=2x\sqrt y volts in the rectangular co-ordinate system. The magnitude of the electric field at x = 1 m, y = 1 m is __ V/m. [1992 1M]

Ans:-  \sqrt5

Explaination: – Electrostatic potential, \theta=2x\sqrt y

\therefore\overrightarrow E\;=-grad\;\left(\theta\right)=-\nabla\theta \therefore\overrightarrow E\;=-\left[{\widehat a}_x\;\frac\partial{\partial x}\;\left(2x\sqrt y\;\right)+{\widehat a}_y\;\frac\partial{\partial y}\;\left(2x\sqrt y\;\right)\right]\; \overrightarrow E\;=\;-{\widehat a}<em>x\;2\sqrt y\;-{\widehat a}</em>{y\;}\frac x{\sqrt y}\;

Now, at x = 1 m and y = 1 m

\overrightarrow E\;=\;-2{\widehat a}_x\;-{\widehat a}_y \therefore \left|\overrightarrow E\right|\;=\;\sqrt{2^2\;+1^2}\;=\sqrt5\;V/m

---

Q.2 Given a vector field \overrightarrow F, the divergence theorem states that [2002 1M]

(a) \int_s\;\overrightarrow F.\;d\overrightarrow s\;=\;\int_v\;\nabla.\;\overrightarrow F\;dV

(b) \int_s\;\overrightarrow F.\;d\overrightarrow s\;=\;\int_v\;\nabla\times\;\overrightarrow F\;dV

(c) \int_s\;\overrightarrow F\times\;d\overrightarrow s\;=\;\int_v\;\nabla.\;\overrightarrow F\;dV

(d) \int_s\;\overrightarrow F\times\;d\overrightarrow s\;=\;\int_v\;\nabla\times\overrightarrow F\;dV

Ans:- (a)

Explanation:- The Divergence Theorem is applicable to the closed surface. It is simply remembered as, the surface integration of the vector field over the closed surface can also be calculated by taking the volume integration of the divergence of that vector field.

---

Q.3 If \overline E is the electric field intensity, \nabla\cdot\left(\nabla\times\overline E\right) is equal to [2005]

(a) \overline E

(b) \left|\overline E\right|

(c) null vector

(d) zero

Ans:- (d)

Explanation:- Divergence of a curl field is zero. This can be easily proved by taking any random vector and applying the successive curl and divergence which will lead to 0.

\nabla\cdot\left(\nabla\times\overrightarrow E\right)\;=0

---

Q.4 Divergence of the vector field

V\left(x,y,z\right)\;=\;-\left(x\;\cos\;xy\;+\;x\right)\;\widehat i\;+\;\left(y\;\cos\;xy\right)\;\widehat j\;+\;\left(\sin\;z^2\;+x^2\;+y^2\right)\;\widehat k is [2007]

(a) 2\;z\;cos\;z^2

(b) \sin\;xy\;+\;2z\;\cos\;z^2

(c) x sin xy – cos z

(d) none of these

Ans:- (a)

Explanation:-
V\left(x,y,z\right)\;=\;-\left(x\;\cos\;xy\;+\;x\right)\;\widehat i\;+\;\left(y\;\cos\;xy\right)\;\widehat j\;+\;\left(\sin\;z^2\;+x^2\;+y^2\right)\;\widehat k

\begin{array}{l}\times\left[\sin\left(Z^2\right)+\left(x^2\right)+\left(y^2\right)\right]\;k\\\end{array}

Divergence is given as

\nabla\cdot V=\frac{\partial V_x}{\partial x}\;+\frac{\partial V_y}{\partial y}\;+\frac{\partial V_z}{\partial z}

= -cos xy + x(sin xy)y + cos xy – y sin(xy)x + 2z cos z²

= \begin{array}{l}2z\;\cos\;z^2\\\end{array}

---

Q.5 The direction of vector A is radially outward from the origin, with \left|A\right|\;=\;kr^n\;where\;r^2=x^2+y^2+z^2 and k is a constant. The value of n for which \nabla\cdot A=0 is [2012]

(a) -2

(b) 2

(c) 1

(d) 0

Ans:- (a)

Explanation :- \begin{array}{l}\overrightarrow A\;=kr^n\;{\widehat i}_r\\\end{array}

\begin{array}{l}\nabla\cdot\overrightarrow A\;=\;\frac1{r^2}\;\frac\partial{\partial r}\;\left(r^2\cdot kr^n\right)\\\end{array} \begin{array}{l}=\;\frac1{r^2}\;\cdot\frac\partial{\partial r}\;\left(kr^{n+2}\right)\\\end{array} \begin{array}{l}=\;\left(n+2\right)k\cdot\frac{r^{n+1}}{r^2}\;=\left(n+2\right)k\;r^{n-1}\\\end{array} \begin{array}{l}\nabla\cdot\overrightarrow A\;=\;0\\n+2=0\\n=-2\\\end{array}

---

Q.6 The following four vector fields are given in Cartesian coordinate system. The vector field which does not satisfy the property of magnetic flux density is

(a) y^2{\widehat a}_x\;+\;z^2{\widehat a}_y\;+\;x^2{\widehat a}_z\;

(b) z^2{\widehat a}_x\;+\;x^2{\widehat a}_y\;+\;y^2{\widehat a}_z\;

(c) x^2{\widehat a}_x\;+\;y^2{\widehat a}_y\;+\;z^2{\widehat a}_z\;

(d) y^2z^2{\widehat a}_x\;+\;x^2z^2{\widehat a}_y\;+\;x^2y^2{\widehat a}_z

Ans :- (c)

Explanation:- We know that the magnetic flux density i.e. B is always in a closed path due to non-existent of the monopole. So according to the Gauss’ Law for magnetic fields we have, \nabla\cdot B=0 (i.e. solenoidal property)

So cheking each option by calculating the divergence when, \overrightarrow B=x^2{\widehat a}_x\;+y^2{\widehat a}_y\;+z^2\;{\widehat a}_z

\nabla\cdot B=2x+2y+2z\;\neq0

---

Q.7 A perfectly conducting metal plate is placed in x – y plane in a right handed coordinate system. A charge of +32\mathrm\pi\in_0\;\sqrt2 Coulomb is placed at co-ordinate (0,0,2). \in_0 is the permittivity of free space. Assume \widehat i,\;\widehat j,\;\widehat k\; to be unit vectors along x, y and z axes respectively. At the co-ordinate \left(\sqrt2,\;\sqrt{2,}\;0\right) , the electric field vector E (Newtons/Coulomb) will be [2014]

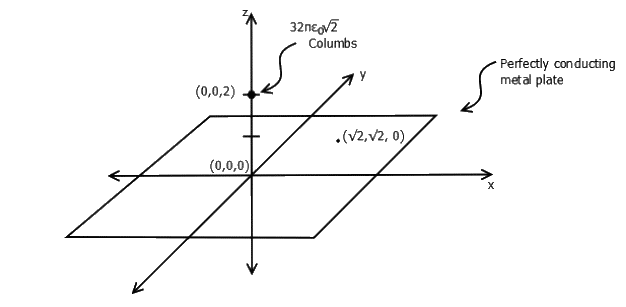
(a) 2\sqrt2\;\widehat k

(b) -2\;\widehat k

(c) 2\;\widehat k

(d) -2\sqrt2\;\widehat k

Ans:- (b)

Explanation:-
According to Image Theory, there is an image of the charge at (0,0,-2). Hence we can say there are two charges. Given +32\mathrm\pi\in_0\;\sqrt2 at (0,0,2) and -32\mathrm\pi\in_0\;\sqrt2 at (0,0,-2).

Total field is {\overrightarrow E}_1+{\overrightarrow E}_2

{\overrightarrow E}_1=\frac{32\mathrm\pi\in_0\;\sqrt2}{4\mathrm\pi\in_0\;\left(2+2+4\right)^{3/2}}\;\left(\sqrt2\;{\widehat a}_x\;+\sqrt2{\widehat a}_y\;-2{\widehat a}_z\right) {\overrightarrow E}_2=\frac{-32\mathrm\pi\in_0\;\sqrt2}{4\mathrm\pi\in_0\;\left(2+2+4\right)^{3/2}}\;\left(\sqrt2\;{\widehat a}_x\;+\sqrt2{\widehat a}_y\;+2{\widehat a}_z\right) \overrightarrow E=-2{\widehat a}_z\;=-2\widehat k\;

---

Q.8 Consider a function \overline f\;=\;\frac1{r^2}\;\widehat r, where r is the distance from the origin and \;\widehat r is the unit vector in the radial direction. The divergence of this function over a sphere of radius R, which includes the origin, is [2015]

(a) 0

(b) \;2\mathrm\pi

(c) \;4\mathrm\pi

(d) \;R\mathrm\pi

Ans:- (c)

Explanation:- \overline f=\frac1{r^2}\;\cdot\widehat r

from divergence theorem as we know,

\int_v\;\left(\nabla\cdot\overline f\right)dv=\oint_s\overline f\cdot d\overline s \oint_s\overline f\cdot d\overline s\;=\oint_s\;\left(\frac1{r^2}\;\cdot\widehat r\right)\;\times r^2\;\sin\;\theta\cdot d\theta\cdot d\phi\cdot\widehat r =\oint_s\sin\;\theta\cdot d\theta\cdot d\phi\;=\left[\int_0^\pi\sin\theta\;d\theta\right]\;\left[\int_0^{2\pi}d\phi\right]=4\mathrm\pi

---

Q.9 In the cylindrical coordinate system, the potential produced by a uniform ring charge is given by f = f(r,z), where f is a continuous function of r and z. Let \overrightarrow E be the resulting electric field. Then the magnitude of \nabla\times\overrightarrow E [2016]

(a) increases with r

(b) is 0

(c) is 3

(d) decreases with z

Ans:- (b)

Explanation:- We know that Electric field is irrotational.

Hence, \nabla\times E=0

---

Q. 10 The line integral of the vector field F=5_xz\widehat i+\left(3x^2+2y\right)\;\widehat j+x^2z\widehat k along a path from (0,0,0) to (1,1,1) parameterized by \left(t,\;t^2,\;t\right) is _. [2016]

Ans :- 4.41

\int_c\;\overline F.\overline dr =\int_c\;5x\;z\;dx+\left(3x^2+2y\right)\;dy\;+x^2\;z\;dz x=t,\;y=t^2,\;z=t,\;t=0\;to\;1

dx = dt; dy = 2tdt, dz = dt

=\int_0^1\;5t^2dt+\left(3t^2+2t^2\right)2t\;dt+t^3dt =\int_0^1\;\left(5t^2+11t^3\right)dt =\left[\frac{5t^3}3\;+\frac{11t^4}4\;\right]_0^1\;=\frac53\;+\frac{11}4\;=\frac{53}{12}\;=4.41

---

Q.11 The figures show diagrammatic representations of vector fields \overrightarrow X,\;\overrightarrow Y,\;\;and\;\;\overrightarrow Z , respectively. Which one of the following choices is true? [2017]

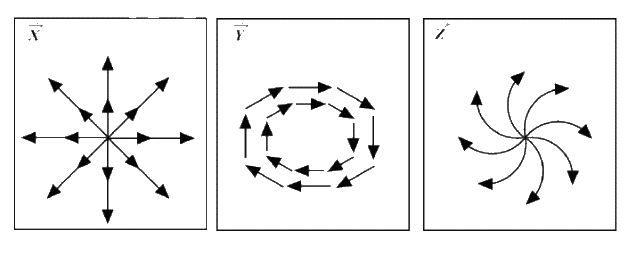
(a) \nabla\cdot\overrightarrow X\;=0,\;\nabla\times\overrightarrow Y\;\neq0,\;\nabla\times\overrightarrow Z\;=0

(b) \nabla\cdot\overrightarrow X\;\neq0,\;\nabla\times\overrightarrow Y\;=0,\;\nabla\times\overrightarrow Z\;\neq0

(c) \nabla\cdot\overrightarrow X\;\neq0,\;\nabla\times\overrightarrow Y\;\neq0,\;\nabla\times\overrightarrow Z\;\neq0

(d) \nabla\cdot\overrightarrow X\;=0,\;\nabla\times\overrightarrow Y\;=0,\;\nabla\times\overrightarrow Z\;=0

Ans:- (c)

Explanation:- \overrightarrow X\;is\;going\;away\;so\;\overrightarrow\nabla\cdot\overrightarrow X\neq0 .

\overrightarrow Y\;is\;moving\;circulator\;direction\;so\;\overrightarrow\nabla\;\times\overrightarrow Y\neq0 \overrightarrow Z\;\;has\;circular\;rotation\;so\;\overrightarrow\nabla\;\times\overrightarrow Z\neq0

---