Boolean Algebra
[1999: 2 M] The logic function f=\overline{\left(x.y\right)+(\overline x.y)} is the same as
a) f=\left(x+y\right)\left(\overline x+\overline y\right)
b) f=\overline{\left(\overline x+\overline y\right)\;\left(x+y\right)}
c) f=\overline{\left(x.y\right)}\;\left(\overline x.\overline y\right)
d) none of the above
Ans: (b)
Explanation
f=\overline{\left(x\cdot\overline y\right)+\left(\overline x\cdot y\right)}=\overline{\left(x\cdot\overline y\right)}\cdot\overline{\left(\overline x\cdot y\right)} =\left(\overline x+y\right)\cdot\left(x+\overline y\right)=xy+\overline x\;\overline ySimplifying option (b) we have,
\overline{\left(\overline x+\overline y\right)\;\left(x+y\right)}=\left(\overline{\overline x+\overline y}\right)+\left(\overline{x+y}\right) =xy+\overline x\;\overline y\;=f[2000: 2 M] The minimal product-of-sum function described by the k-map given in figure, is
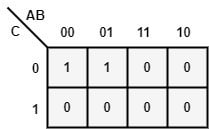
a) A’ C’
b) A’ +C’
c) A+C
d) AC
Ans: (a)
Explanation
[2003: 2 M] The Boolean expression \overline XY\overline Z+\overline X\;\overline Y\;Z+X\overline YZ+XYZ\; can be simplified to
a) X\overline Z+\overline XZ+YZ
b) XY+\overline YZ+Y\overline Z
c) \overline XY+YZ+XZ
d) \overline{XY}+Y\overline Z+\overline XZ
Ans: (b)
Explanation
Let us present given expression in the k-map.
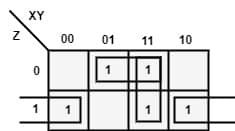
After simplification, XY+Y\overline Z+\overline YZ
[2004: 2 M] The simplified form of the Boolean expression Y=\left(\overline ABC+D\right)\;\left(\overline AD+\overline B\;\overline C\right) can be written as
a) \overline AD+\overline B\;\overline CD
b) AD+B\overline CD
c) \left(\overline A+D\right)\left(\overline BC+\overline D\right)
d) A\overline D\;+BC\overline D
Ans: (a)
Explanation
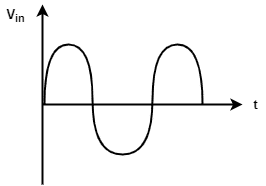
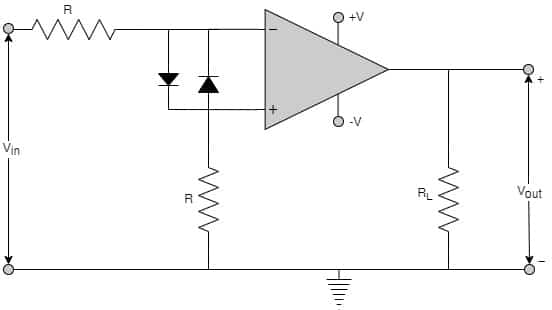
Y=\left(\overline ABC+D\right)\;\left(\overline AD+\overline B\;\overline C\right) =\overline A\;BC\overline AD+\overline A\;BC\overline B\;\overline C+\overline A\;D+\overline B\;\overline C\;D =\overline A\;BCD+0+\overline A\;D+\overline B\;\overline C\;D =\overline A\;D(BC+1)+\overline B\;\overline C\;D =\overline A\;D+\overline B\;\overline C\;D[2005: 2 M] In the given figure, if the input is a sinusoidal signal, the output will appear as shown in diagram
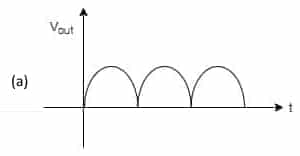
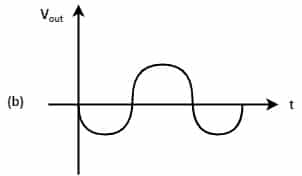
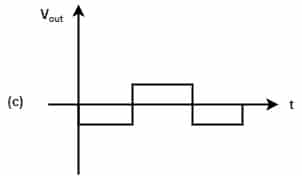
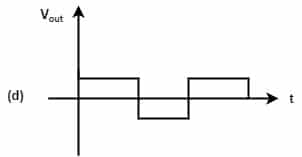
Ans: (c)
Explanation
As Op-amp is in open loop, output will be at its saturation values.
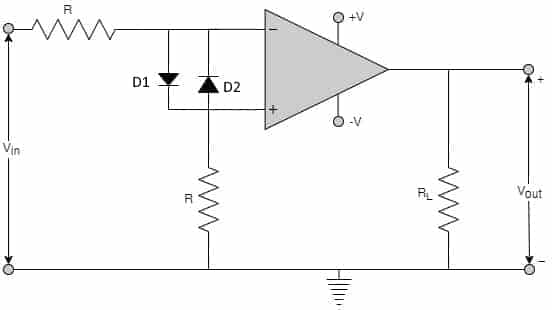
For +ve half of the input, D1 will conduct. Hence, voltage at negative terminal of op-amp is vin while voltage at positive terminal will be (vin ‒ 0.7). In other words, negative terminal of op-amp is 0.7V higher than positive terminal. So, output will be -Vsat.
On the similar lines, for -ve half of the input, D2 will conduct. Hence, voltage at positive terminal of op-amp is vin while voltage at negative terminal will be (vin ‒ 0.7). In other words, positive terminal of op-amp is 0.7V higher than negative terminal. So, output will be +Vsat.
[2010] Statement for linked Answer Questions
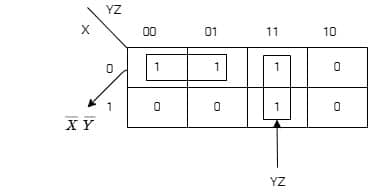
The following Karnaugh map represents a function F.
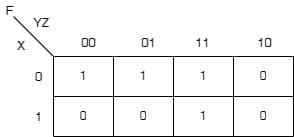
[2010: 2 M] A minimized form of the function F is
a) F=\overline XY+YZ
b) F=\overline X\;\overline Y+YZ
c) F=\overline X\;\overline Y+Y\overline Z
d) F=\overline X\;\overline Y+\overline YZ
Ans: (b)
Explanation
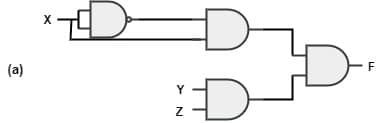
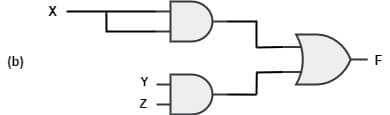
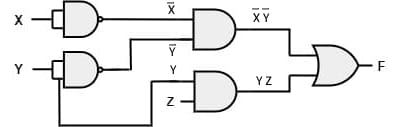
[2010: 2 M] Which of the following circuits is a realization of the above function F?
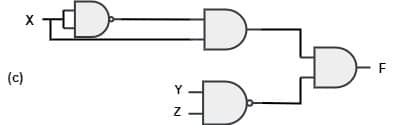
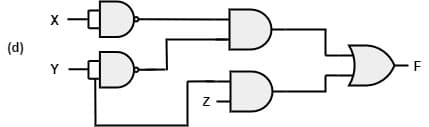
Ans: (d)
Explanation
NAND gate with same input acts as an inverter. So, the from figure(d), it is clear that, two NAND gates generate the \overline X and \overline Y.
Two AND gates with i/ps \overline X and \overline Y and inputs Y and Z in addition with OR gate is used to generate two terms of SOP form and generate the F.
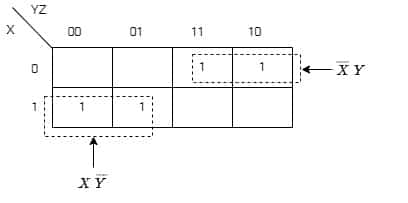
[2012: 1 M] In the sum of products function: f\left(X,\;Y,\;Z\right)=\sum\left(2,\;3,\;4,\;5\right) the prime implicants are
a) \overline XY+X\overline Y
b) \overline XY+X\overline Y\;\overline Z+X\overline YZ
c) \overline XY\overline Z+\overline XY\;Z+X\overline Y
d) \overline XY\overline Z+\overline XY\;Z+X\overline Y\;\overline Z+X\overline YZ
Ans: (a)
Explanation
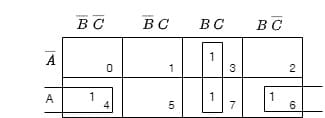
f(X, Y, Z)= Σ(2, 3, 4, 5)
[2014: 1M, Set-2] Which of the following is an invalid state in 8-4-2-1 Binary Coded Decimal counter
a) 1 0 0 0
b) 1 0 0 1
c) 0 0 1 1
d) 1 1 0 0
Ans: (d)
Explanation
Binary coded decimal counter counts from 0 to 9. So, 1100 is an invalid state i.e. 12.
[2014: 2 M, Set-2] The SOP (sum of products) form of a Boolean function is Σ(0, 1, 3,7, 11), where inputs are A, B, C, D(A is MSB, and D is LSB). The equivalent minimized expression of the function is
a) \left(\overline B+C\right)\;\left(\overline A+C\right)\;\left(\overline A+\overline B\right)\;\left(\overline C+D\right)
b) \left(\overline B+C\right)\;\left(\overline A+C\right)\;\left(\overline A+\overline C\right)\;\left(\overline C+D\right)
c) \left(\overline B+C\right)\;\left(\overline A+C\right)\;\left(\overline A+\overline C\right)\;\left(\overline C+\overline D\right)
d) \left(\overline B+C\right)\;\left(A+\overline B\right)\;\left(\overline A+\overline B\right)\;\left(\overline C+D\right)
Ans: (a)
Explanation
The 4 variable Boolean function is given in canonical (SOP) sum of products form as, f(A, B, C,D)=Σ(0, 1, 3, 7, 11)
But, the options are given in the simplified (POS) product of sums form. So, convert the given function in canonical product of sums form,
f(A, B, C, D)= Π(2, 4, 5, 6, 8, 9, 10, 12, 13, 14, 15)
Plotting the above function on a 4 variable K-map (Maxterms map), we obtain the simplified expression of the function
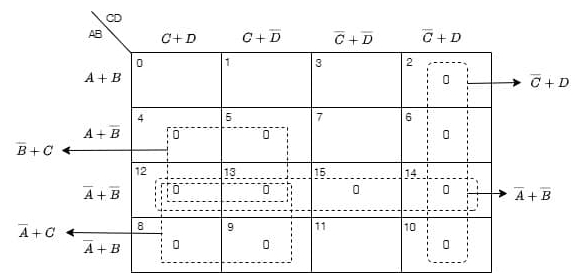
[2015: 2 M, Set-1] f(A, B, C, D) = Π M(0,1, 3, 4, 5, 7, 9, 11, 12, 13, 14, 15) is a maxterm representation of Boolean function f(A, B, C, D) where A is the MSB and D is the LSB. The equivalent minimized representation of this function is
a) \left(A+\overline C+D\right)\;\left(\overline A+B+D\right)\;
b) A\overline CD+\overline ABD
c) \overline AC\overline D+A\overline BC\overline D+A\overline B\;\overline C\;\overline D
d) \left(B+\overline C+D\right)\left(A+\overline B+\overline C+D\right)\left(\overline A+B+C+D\right)
Ans: (a)
[2015: 1 M,Set-2] Consider the following Sum of Products expression, F.
F=ABC+\overline A\;\overline BC+A\overline BC+\overline ABC+\overline A\;\overline B\;\overline CThe Equivalent Product Of Sums expression is
a) F=\left(A+\overline B+C\right)\left(\overline A+B+C\right)\left(\overline A+\overline B+C\right)
b) F=\left(A+\overline B+\overline C\right)\left(A+B+C\right)\left(\overline A+\overline B+\overline C\right)
c) F=\left(\overline A+B+\overline C\right)\left(A+\overline B+\overline C\right)\left(A+B+C\right)
d) F=\left(\overline A+\overline B+C\right)\left(A+B+\overline C\right)\left(A+B+C\right)
Ans: (a)
Explanation
The expression SOP in k-map is given as
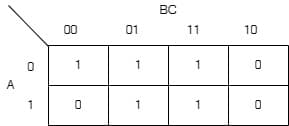
So, POS form can be formed using ‘0’s from the K-map
POS=F=\left(A+\overline B+C\right)\left(\overline A+B+C\right)\left(\overline A+\overline B+C\right)
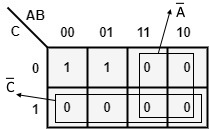
[2016: 1 M, Set-2] The output expression for the Karnaugh map shown below is
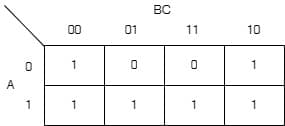
a) A+\overline B
b) A+\overline C
c) \overline A+\overline C
d) \overline A+C
Ans: (b)
Explanation
[2016: 2 M, Set-2] The Boolean expression: \overline{\left(a+\overline b+c+\overline d\right)+\left(b+\overline c\right)} simplifies to
a) 1
b) \overline{a.b}
c) a, b
d) 0
Ans: (d)
Explanation
F=\overline{\left(a+\overline b+c+\overline d\right)+\left(b+\overline c\right)} =\overline{\left(a+\overline b+c+\overline d\right)}\cdot\overline{\left(b+\overline c\right)} =\overline a\cdot b\cdot\overline c\cdot d\cdot\overline b\cdot c= 0
[2017: 1 M, Set-1] The Boolean expression, AB+A\overline C+BC simplifies to
a) BC+A\overline C
b) AB+A\overline C+B
c) AB+A\overline C
d) AB+BC
Ans: (a)
Explanation
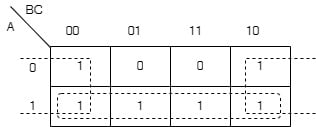
[2017: 2 M, Set-1] The output expression for the Karnaugh map shown below is
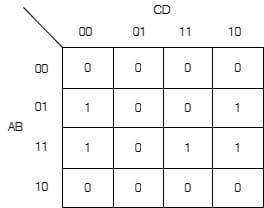
a) B\overline D+BCD
b) B\overline D+AB
c) \overline BD+ABC
d) B\overline D+ABC
Ans: (d)
Explanation
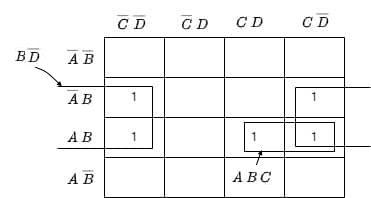
[2018: 2 M] Digital input signals A, B, C with A as the MSB and C as the LSB are used to realize the Boolean function F=m0+m2+m3+m5+m7, where mi denotes the Ith minterm. In addition, F has a don’t care for m1. The simplified expression for F is given by
a) \overline A\;\overline C+\overline BC+AC
b) \overline A\;+C
c) \overline C\;+A
d) \overline AC\;+BC+A\overline C
Ans: (b)
Explanation
Putting the given minterms in k-map