Rotational Dynamics 2023-2019

March 2023

Q. If friction is made zero for a road, can a vehicle move safely on this road?

Answer:

No.

It will skid in the absence of friction.

---

Q. Derive expressions for linear velocity at lowest position, mid-way position and the top-most position for a particle revolving in a vertical circle, if it has to just complete circular motion without string slackening at top.

Answer:

Consider a body (small heavy sphere) of mass m tied to one end of the string & revolved in vertical circle of radius r as shown.

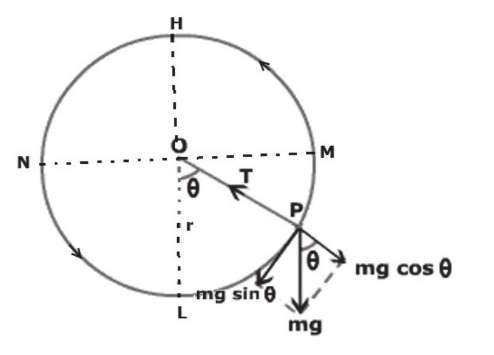
Let the particle be at point P so that angle LOP = θ.

During its motion, the forces acting on body are as: –

1. Its weight mg acting vertically downwards &
2. Tension T in the string directed towards the centre O of the circle.

Resolving the weight mg into two components: –

a) m g \cos \theta, along the string &

b) m g \sin \theta, right angles to the string.

The component (m g \sin \theta) opposes the upward motion of the body.

Hence the velocity of the body goes on decreasing as it rises from its lowest position L to the highest position \mathrm{H} along LMH.

On the other hand, during the downward motion along \mathrm{HNL}, the component m g \sin \theta acts in the same direction as that of the motion & hence velocity of the body goes on increasing along the path BDA.

Thus it is clear that in vertical circular motion, the velocity of the body goes on changing both in magnitude as well as in direction. Hence vertical circular motion is nonuniform circular motion.

The component m g \cos \theta opposes the tension in the string. Hence resultant force acting on body in the direction PO is (T-m g \cos \theta). This is directed along the radius towards the centre of the circle & it acts as centripetal force \left(m v^{2} / r\right).

\therefore T-m g \cos \theta=\frac{m v^{2}}{r} \therefore T=\frac{m v^{2}}{r}+m g \cos \theta

i. At highest point H

At highest point \mathrm{H}, \theta=180^{\circ} \therefore \cos \theta=-1 .

Hence \mathrm{T} will be minimum and given by,

T_{\min }=\frac{m v^{2}}{r}-m g

The minimum Tension in the string can be zero.

T_{min}=\frac{mv_{H}^{2}}{r}-mg \therefore\frac{mv_H^2}r=mg \therefore v_H^2=gr \therefore v_H=\sqrt{gr}

This is the minimum velocity at the highest point.

ii. At Lowest point L

At lowest point \mathrm{L}, \theta=0^{0} \therefore \cos \theta=1 .

Hence \mathrm{T} will be maximum and given by,

T_{\max }=\frac{m v^{2}}{r}+m g

Now, let us find velocity at L utilizing law of conservation of energy. The potential energy at point \mathrm{L} is zero.

As the particle moves from point L to the H , it is raised to a vertical distance L O H=2 r .

According to law of conservation of energy,

total energy at L= total energy at H

\frac{1}{2} m v_{L}^{2}=\frac{1}{2} m v_{H}^{2}+m g(2 r) \frac12mv_L^2=\frac12m(\sqrt{gr})^2+mg(2r) \frac{1}{2} m v_{L}^{2}=\frac{1}{2} m g r+2 m g r=\frac{5}{2} m g r \therefore v_{L}=\sqrt{5 g r}

This is the minimum velocity at the lowest point.

iii. At Point M

In the position M, the particle is raised to a vertical distance r, hence according to the law of conservation of energy,

total energy at M = Total energy at L

\therefore \frac{1}{2} m v_{M}^{2}+m g r=\frac{1}{2} m v_{L}^{2} \therefore \frac{1}{2} m v_{M}^{2}+m g r=\frac{1}{2} m(5 g r) \quad \text { as } v_{L}=\sqrt{5 g r} \therefore \frac{1}{2} m v_{M}^{2}=\frac{5}{2} m g r-m g r=\frac{3}{2} m g r \quad \therefore v_{M}^{2}=3 g r \therefore v_{M}=\sqrt{3 g r}

This is the minimum velocity at the middle point.

---

Q. State and prove principle of conservation of angular momentum.

Answer:

Law of conservation of angular momentum :

If no external torque acts on rotating body, then its angular momentum remains conserved (constant).

Proof :

When torque (τ) is applied on the body of M. I. (I) then it rotates with an angular acceleration (α),

i.e. τ = I α

\therefore \tau=I\frac{d \omega}{d t} \quad as, \alpha=\frac{d \omega}{d t}

\therefore \tau = \frac{d(I \omega)}{dt} as, I is constant

\therefore \tau = \frac{dL}{dt} as L = I ω

As no torque acts on the body, we have, τ = 0, hence we have,

Thus, angular momentum of the body remains constant if no torque acts on body.

Examples :

a) Ballet dancers fold their arms for decreasing the M.I. and hence to
increase the angular Speed. Similarly they pull out arms to increase the M.I. or to
decrease the speed.

b) A diver pulls in arms and legs in the start of the dive to decrease the M.I. or to
increase the angular speed.

---

March 2022

Q. Define moment of inertia of a rotating rigid body. State its SI unit and dimensions.

Answer:

Moment of inertia [ M. I. ( I ) ] :

The moment of inertia of a body about a given axis of rotation is defined as the sum of products of the masses of each particle & the square of its distance from the axis of rotation.

Explanation :

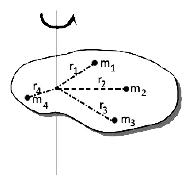
Consider a rigid body consisting of n particles of masses m₁ , m₂ , . . . . . m_n situated at distances r₁ , r₂ , . . . . . . r_n respectively from axis of rotation.

Let it be rotating about an axis as shown. Then moment of inertia (I) of the body about the axis of rotation is,

I=m_1r_1^2 + m_2r_2^2 +\;.\;.\;.\;. +m_nr_n^2 \therefore I = \sum_{i=1}^{n}m_ir_i^2

S.I. unit of M.I. is kg-m² & CGS unit of M.I. is g-cm² and dimensions are [ M¹L²T⁰ ]

---

Q. Derive an expression for the kinetic energy of a body rotating with a uniform angular speed.

Answer:

Consider a rigid body rotating about an axis passing through O with constant angular velocity ω. Let it consists of n particles of masses m₁ , m₂ , m₃ . . . . . m_n at distances r₁ , r₂ , . . . . . . r_n respectively from axis of rotation. As the body is rigid, every particle rotates with same angular velocity ω.

As the body rotates, the particle of mass m₁ revolves along the circle of radius r₁ . The linear velocity of the particle is v₁ = r₁ ω . Hence its kinetic energy (E₁) is given by,

E_1=\frac{1}{2}m_1v_1^2=\frac{1}{2}m_1(r_1\omega)^2=\frac{1}{2}m_1r_1^2\omega^2

Similarly for other particles, we have,

E_2=\frac{1}{2}m_2r_2^2\omega^2,\;\;\;E_3=\frac{1}{2}m_3r_3^2\omega^2,\;.\;.\;.\;.\;E_n=\frac{1}{2}m_nr_n^2\omega^2

Hence total K.E. of rotating body is given by,

E = E₁ + E₂ + E₃ + . . . . . + E_n

= \frac{1}{2}m_1r_1^2\omega^2+\frac{1}{2}m_2r_2^2\omega^2+.\;.\;.\;.\; \frac{1}{2}m_nr_n^2\omega^2

= \frac{1}{2} \left[m_1r_1^2\omega^2+m_2r_2^2\omega^2+\;.\;.\;.\;m_nr_n^2\omega^2 \right]

= \frac{1}{2}\left[m_1r_1^2+m_2r_2^2+\;.\;.\;.m_nr_n^2 \right] \omega^2=\frac{1}{2}\left[\sum_{i=1}^{n}m_ir_i^2 \right]\omega^2

\therefore E = \frac{1}{2}I \omega^2

---

Q. Calculate the moment of inertia of a uniform disc of mass 10kg and radius 60cm about an axis perpendicular to its length and passing through its centre.

Answer: M. I. of uniform disc about an axis perpendicular to its length and passing through its centre,

I=\frac12MR^2=\frac12\times10\times\left(0.6\right)^2=5\times0.36 \therefore I=1.8\;kg\;m^2

---

March 2020

Q. In rotational motion of a rigid body, all particles move with ____.

(a) same linear velocity and same angular velocity

(b) same linear velocity and different angular velocity

(c) different linear velocities and same angular velocities

(d) different linear velocities and different angular velocities

Answer: (c)

---

Q. Define uniform circular motion.

Answer:

Uniform circular motion (U.C.M.):

The motion of the particle along the circumference of the circle with constant speed (constant angular velocity) is called uniform circular motion.

---

Q. State and prove the principle of parallel axes in rotational motion.

Answer:

Principle (or theorem) of Parallel axes :

Statement :

The M. I. of a body about any axis (I_o) is equal to the sum of its M I. about a parallel axis passing through its center of mass (I_c) & the product of mass
of the tody (M) & square of the distance (h) between the tvvo axes i.e. I_o = I_c + Mh²

Proof :

Consider a rigid body rotating about an axis passing through a point O as shown.
The axis is perpendicu1ar to the plane of figure.

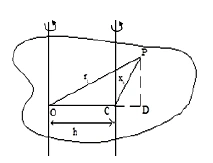
Consider the i^th panicle of mass m_i is located at point P at distance r_i from this axis. A parallel axis passes through the point C, which is center of mass of the body.

The particle is at a distance x_i from C. Let h the distance between two parallel
axes. Draw a perpendicular PD from P on OC produced.

The M I. of the body about an axis passing through point ‘O’ is given by,

I_O=\sum_{i=1}^n m_i r_i^2 – – – – – (i)

From figure, we have,

O P^2 =O D^2+P D^2=(O C+C D)^2+P D^2 =O C^2+2 O C \cdot C D+C D^2+P D^2 =O C^2+2 O C \cdot C D+C P^2 \therefore r_i^2 =h^2+2 h \cdot C D+x_i^2

Thus equation (i) becomes,

I_O =\sum_{i=1}^n m_l\left(h^2+2 h \cdot C D+x_i^2\right)=\sum_{i=1}^n\left(m_i h^2+2 h \cdot C D m_i+m_i x_i^2\right) =h^2 \sum_{i=1}^n m_i+2 h \sum_{i=1}^n C D \cdot m_i+\sum_{i=1}^n m_i x_i^2 =h^2 M+0+I_C

as, \sum_{i=1}^{n}m_i= M = Mass of the body

& \sum_{i=1}^{n}CD. m_i = 0, as C is Centre of mass

also \sum_{i=1}^{n}m_ix_i^2 = M.I. of the body about an parallel axis passing through point C = I_c

\therefore I_o = I_c + Mh^2

---

Q. In a Circus, a motor-cyclist having mass of 50 kg moves in a spherical cage of radius 3 m. Calculate the least velocity with which he must pass the highest point without losing contact. Also calculate his angular speed at the highest point.

Answer:

m = 50 kg, r = 3 m

i) velocity at highest point (\left(V_H\right))

ii) Angular velocity at highest point (\omega)

i) V_H=\sqrt{rg}

ii) V_H=r\omega

Using formula (i),

V_H=\sqrt{3\times9.8} \therefore V_H=5.42\;m/s

Using formula (ii),

\omega=\frac{V_H}r=\frac{5.42}3 \therefore\omega=1.8\;rad/s

The least velocity with which the motor cyclist must pass the highest is 5.42 m/s and the angular velocity at the highest point is 1.8 rad/s.

---

Q. Energy of 1000 J is spent to increase the angular speed of a wheel from 20 rad/s to 30 rad/s. Calculate the moment of inertia of the wheel.

Answer:

n_1=20\;r.p.s.,

n_2=30\;r.p.s.,

\triangle E=1000J

Moment of inertia (1)

K.E=\frac12I\omega^2

From formula,

{\left(K.E\right)}_1=\frac12\times I\times\left(2\pi n_1\right)^2=2\pi^2n_1^2I

Similarly,

{\left(K.E\right)}_2=2\pi^2n_1^2I \triangle E={\left(K.E\right)}_2-{\left(K.E\right)}_1 =\left(2\pi^2n_2^2-2\pi^2n_1^2\right)1 \therefore\triangle E=2\pi^2\left(n_2^2-n_1^2\right)I \therefore I=\frac{\triangle E}{2\pi^2\left[n_2^2-n_1^2\right]} =\frac{1000}{2\left(3.142\right)^2\left[\left(30\right)^2-\left(20\right)^2\right]} \therefore I=0.1013\;kg\;m^2

The moment of inertia of the wheel is 0.1013\;kg\;m^2

---

March 2019

Q. What is the value of tangential acceleration in U.C.M.?

Answer:

It is always ZERO in UCM.

---

Q. Define radius of gyration. Write its physical significance.

Answer:

Radius of gyration ( K ) :

The radius of gyration of a body about a given axis of rotation is &fined as the
distance between axis of rotation & a point at which whole mass of the body is
supposed to be concentrated so as to possess the same M. I. as that of the body.

Explanation :

Consider a disc of mass M rotating about an axis passing through its center & perpendicular to its plane as shown. Let I be the MI. of the disc.

Suppose the disc is now replaced by a single particle of same mass (M) as that
of the disc. This particle is at a distance K from axis of rotation. It gives same M.l.
as that of the disc. The distance K is called the radius of gyration.

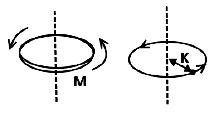
Thus M.I. of the particle which is same as that of body is, I = MK².

Physical significance of radius of gyration :

I) The radius of gyration of a body depends upon, (a) Mass of the body and (b) Distribution of mass about the axis of rotation.

Thus, radius of gyration (K) saves as an indication of the distribution of mass about the axis of rotation.

2) If distribution of mass of the body is closer to the axis of rotation then the value of K is small.

3) If the distribution of mass of the body is away from the axis of rotation then the value of K is large.

---

Q. The radius of gyration of a body about an axis, at a distance of 0.4 m from its centre of mass is 0.5 m.  Find its radius of gyration about a parallel axis passing through its centre of mass.

Answer:

Radius of gyration about given axis parallel to the axis passing through centre of mass is,

K_p=0.5\;m

Distance between two axes h = 0.4 m

from parallel axes therom,

I_P=I_C+Mh^2 \therefore MK_P^2=MK_C^2+Mh^2 \therefore K_C^2=K_P^2-h^2 \therefore K_C=\sqrt{K_P^2-h^2} =\sqrt{\left(0.5\right)^2-\left(0.4\right)^2} =\sqrt{0.25-0.16} =\sqrt{0.09}=0.3\;m

The radius of gyration about axis passing through the centre of mass is 0.3 m.

---

Q. A wheel of moment of inertia 1 kg m² is rotating at a speed of 30 rad/s. Due to friction on the axis, it comes to rest in 10 minutes. Calculate the average torque of the friction.

Answer:

I=1\;kg\;m^2,

n = 40 rad/s

t_1=600\;s t_2=10-2=8\;min=480\;s \omega_1=40\;rad/s

Angular momentum (L)

i) \omega_2=\omega_1+\alpha t

ii) L=I\omega

From formula (i),

\omega_2=\omega_1+\alpha t_1\\ 0=40+600\;\alpha\\ \therefore\alpha=\frac{-1}{15}rad/s^2\\ \therefore\omega_3=8\;rad/s\\

From formula (ii)

L=I\omega_3=1\times8=8\;kg\;m^2/s\\

The angular momentum of the wheel, two minutes before it comes to rest would be 8\;kg\;m^2/s\\