What is Steady State Stability of an Induction Motor ?

In the field of electrical engineering, the concept of induction motor has a very significant importance. From powering industrial machinery to driving the wheels of electric vehicles, these workhorses of the electrical world play a vital role in our daily lives.

Have you ever imagined a world where the electricity supply to our homes and industries was anything but stable. Lights flicker, machines grind to a halt, and the comfort of modern life hangs in the balance. To prevent such chaos, understanding the steady-state stability of induction motors is of utmost importance.

In this article, we will understand the concept of Steady State Stability of an Induction Motor in detail.

Induction Motor

Induction motor is invented by Nikola Tesla . Induction Motors are electric motors that use alternating current (AC), propelled by a magnetic field that rotates.

They are made up of a rotor, a stator and coils that convert electrical energy into mechanical energy using electromagnetic induction. AC induction motors are highly efficient and flexible, and relatively simple in design, which allows them to match the load demand for almost any electrical application.

A stator is an outer, non-moving chamber in which the rotor spins. A rotor also consists of a group of electromagnets arranged around a cylinder, and it is housed inside the stator.

Types of Induction Motor

There are basically two types of induction motor :-

i) Single-phase Induction Motor – It is not self starting

ii) Three-Phase Induction Motor – It is self starting

Steady State Stability of an Induction Motor

Steady State Stability Evaluates stability of an equilibrium point from the speed-torque characteristics.

Steady-state stability in an induction motor is the capability to maintain a consistent speed and torque output under normal operating conditions. It is crucial for reliable and efficient motor operation in industrial settings.

Achieving steady-state stability involves factors such as proper design, maintenance, control, and protection measures to ensure that the motor operates smoothly and without instability or damage.

Let us firstly understand, the concept of steady state and dynamic state.

i) Steady State :- In steady state, motor torque = Load Torque = Equilibrium speed is obtained

T_{M}-T_{L}=J\frac{d\omega }{dt}=0

T_M– T_L =0

T_M = motor torque

T_L = load torque

J = moment of inertia

\frac{d\omega }{dt}=0 = change in speed

T_M = T_L

This state is called as Steady State.

The motor should operate on steady state only.

ii) Dynamic State :- In dynamic state,

T_{M}-T_{L}=J\frac{d\omega }{dt}

Let us understand this with the help of curve below.

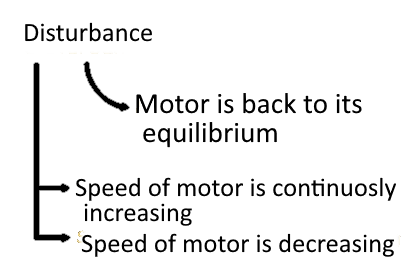
Suppose there is a some kind of disturbance in the motor, while there is disturbance in the motor, if motor is back to its equilibrium, then the state is called as stable state.

The other state is called as unstable if the motor speed is :-

i) continuously increasing

ii) Continuously decreasing

When the motor is operating it should come back to its equilibrium, this condition is referred as Stable state.

Let us see one by one the operation of region

i) Stable Operating region – Consider the dynamic equation

T_{M}-T_{L}=j\frac{d\omega }{dt}

Due to any disturbance, there is a difference between T_m and T_L. \frac{d\omega }{dt} is not equal to zero. So, the ω , may increase or decrease.

Let us consider two cases,

Case-1 :– When ω (speed) increases, T_L (load torque) > T_M (motor torque) will deaccelerate.

Case-2 :- When ω (speed) decreases, T_L < T_M will accelerate.

ii) Unstable Operating region – The equation is given by,

T_{M}-T_{L}=j\frac{d\omega }{dt}

When ω (speed) increases, T_M (motor torque) > T_L (load torque), the motor will accelerate.

When ω (speed) decreases, T_M (motor torque) < T_L (load torque) , the motor will deaccelerate.

This is unstable operation.

Now let us see how to determine, whether system is stable or unstable. We will understand this with the help of curves.

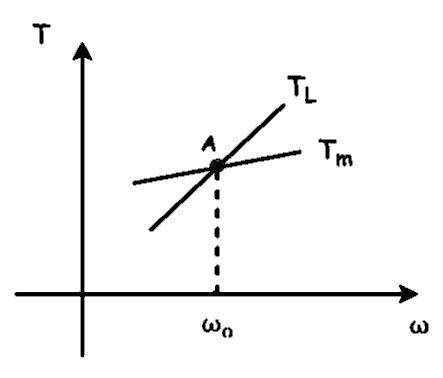
ω_o = equillibrium speed of the motor

We know the equation,

T_{M}-T_{L}=j\frac{d\omega }{dt}

When speed will increase, the load torque is greater than motor torque, so, motor will deaccelerate.

When speed will decrease, the load torque is less than the motor torque. So, motor will accelerate

From the curve, point A is the stable point.

Now, consider another curve,

Consider the point , B. the dynamic equation is T_{M}-T_{L}=j\frac{d\omega }{dt}

Here also consider two cases,

Case-1 :- When speed will increase, the motor torque is greater than load torque, so, motor will accelerate.

Case-2 :- When speed will increase, the load torque is greater than motor torque, so, motor will deaccelerate.

These point B is undesirable point as it is showing unstable operation.

Now, concluding the concept of steady state stability, we get that

When the system is stable, change in load torque is greater than change in motor torque in case of increase in speed.

change in load torque is smaller than change in moto torque in case of decrease in speed.

In this cases, we can say that system is stable.

Hope, so , that the concept of steady state stability is cleared to you.