The del operator is useful for finding Gradient, Divergence, Curl and Laplacian. Let us discuss how can we get the cylindrical Del operator from its Cartesian formula.
What is the Del Operator?
It is a vector differentiation tool. It is significant in Electromagnetics for finding Gradient, Divergence and Curl. In a cartesian coordinate system it is defined as follows:-
\nabla={\overrightarrow a}_x\frac\partial{\partial x}+{\overrightarrow a}_y\frac\partial{\partial y}+{\overrightarrow a}_z\frac\partial{\partial z}As you can see from the above formula, it is a vector differential operator. It can be operated on a scalar or a vector field and depending on the operation the outcome can be a scalar or vector. For example, if it is operated on a scalar field, the operation is known as Gradient whose answer is a vector. For the vector fields, its application yields two operations namely Divergence and Curl. The outcome of the Divergence of a vector field is a scalar while that of Curl is a vector.
Now, in our Eletcromagnetics, we generally use three types of coordinate systems viz. Cartesian, Cylindrical and Spherical. So it is quite obvious that to convert the Cartesian Del operator above into the Cylindrical Del operator and Spherical Del operator.
Conversion from Cartesian to Cylindrical
Let me present the formula for the del operator in Cartesian Coordinate System which we are going to convert into other system.
\nabla={\overrightarrow a}_x\frac\partial{\partial x}+{\overrightarrow a}_y\frac\partial{\partial y}+{\overrightarrow a}_z\frac\partial{\partial z}And the same del operator in Cylindrical Coordinate System is as follows: –
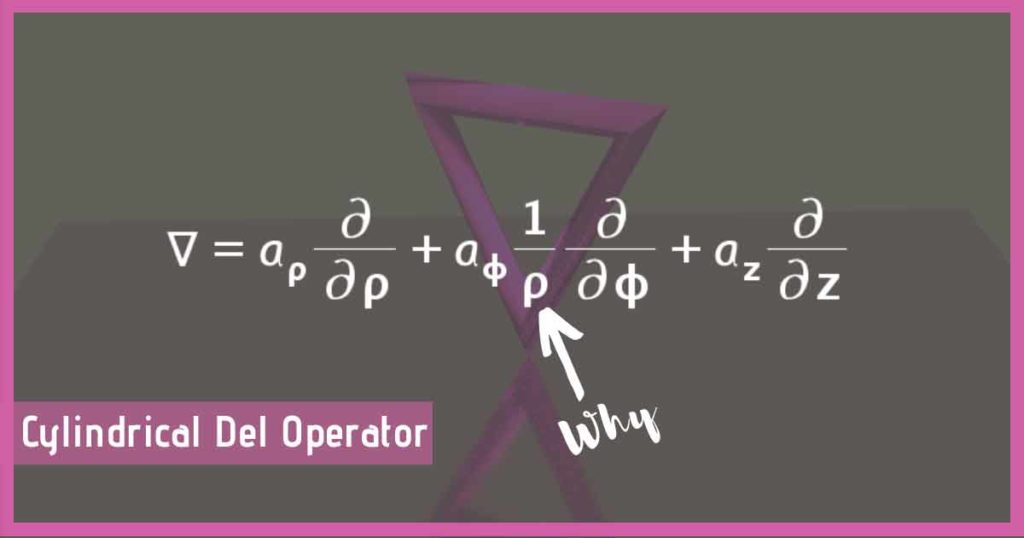
\nabla={\overrightarrow a}_{\rho}\frac\partial{\partial\rho}+{\overrightarrow a}_{\phi}\frac1\rho\frac\partial{\partial\phi}+{\overrightarrow a}_z\frac\partial{\partial z}Let us work mathematically to prove that both are the same.
First of all, as we are trying to convert the formula from Cartesian to Cylindrical, let us recall the transformation formulas between these coordinate systems. We know that, Cartesian coordinate System is characterized by x, y and z while Cylindrical Coordinate System is characterized by ρ, φ and z. The conversion formulas are as follows:-


Again have a look at the Cartesian Del Operator. To convert it into the cylindrical coordinates, we have to convert the variables of the partial derivatives. In other words, in the Cartesian Del operator the derivatives are with respect to x, y and z. But Cylindrical Del operator must consists of the derivatives with respect to ρ, φ and z. So let us convert first derivative i.e.
\frac\partial{\partial x}\Rightarrow in\;terms\;of\;\frac{\displaystyle\partial}{\displaystyle\partial\rho};\frac{\displaystyle\partial}{\displaystyle\partial\phi}\;and\;\frac{\displaystyle\partial}{\displaystyle\partial z}For that let us apply the basic rule of the differentiation called the chain rule.
\frac\partial{\partial x}=\frac{\displaystyle\partial}{\displaystyle\partial\rho}\frac{\displaystyle\partial\rho}{\displaystyle\partial x}+\frac{\displaystyle\partial}{\displaystyle\partial\phi}\frac{\displaystyle\partial\phi}{\displaystyle\partial x}Note here that in the the above formula I have skipped the variable z. The reason behind this is very simple. As we know for both the systems i.e. Cartesian and Cylindrical z coordinate is exactly the same only ρ and φ are the functions of x and y as mentioned above.
\frac{\displaystyle\partial\rho}{\displaystyle\partial x}=\frac{\displaystyle\partial}{\displaystyle\partial x}\left(\sqrt{x^2+y^2}\right)=\frac x{\sqrt{x^2+y^2}} \therefore\frac{\displaystyle\partial\rho}{\displaystyle\partial x}=\frac{\rho\cos\phi}\rho=\cos\phiNote the simplification in the above step. As we are going to convert into the Cylindrical coordinates from the Cartesian ones, we must simplify to the extent so that to get cylindrical variables. Similarly,
\frac{\displaystyle\partial\phi}{\displaystyle\partial x}=\frac{\displaystyle\partial}{\displaystyle\partial x}\tan^{-1}\left(\frac yx\right)=\frac{-y}{x^2}\frac1{1+\left(y/x\right)^2}=\frac{-y}{x^2+y^2} \therefore\frac{\displaystyle\partial\phi}{\displaystyle\partial x}=\frac{-\rho\sin\phi}{\rho^2}=-\frac{\sin{\displaystyle\phi}}\rhoSo putting these values above, we have,
\frac\partial{\partial x}=\left(\cos\phi\right)\frac{\displaystyle\partial}{\displaystyle\partial\rho}+\left(\frac{\displaystyle-\sin\phi}\rho\right)\frac{\displaystyle\partial}{\displaystyle\partial\phi}Working on the similar lines, we have,
\frac\partial{\partial y}=\left(\sin\phi\right)\frac{\displaystyle\partial}{\displaystyle\partial\rho}+\left(\frac{\displaystyle\cos\phi}\rho\right)\frac{\displaystyle\partial}{\displaystyle\partial\phi}Now, let’s collect all things together.
\nabla={\overrightarrow a}_x\frac\partial{\partial x}+{\overrightarrow a}_y\frac\partial{\partial y}+{\overrightarrow a}_z\frac\partial{\partial z} \therefore\nabla=\left(\cos\phi\;a_\rho-\sin\phi\;a_\phi\right)\left(\left(\cos\phi\right)\frac\partial{\partial\rho}+\left(\frac{-sin\phi}\rho\right)\frac\partial{\partial\phi}\right) +\left(\sin\phi\;a_\rho+\cos\phi\;a_\phi\right)\left(\left(\sin\phi\right)\frac\partial{\partial\rho}+\left(\frac{\cos\phi}\rho\right)\frac\partial{\partial\phi}\right)+{\overrightarrow a}_z\frac\partial{\partial z}Collecting similar terms together we get as follows: –
\nabla=\left(\sin^2\phi+\cos^2\phi\right){\overrightarrow a}_{\rho}\frac\partial{\partial\rho}+\frac1\rho\left(\sin^2\phi+\cos^2\phi\right){\overrightarrow a}_{\phi}\frac\partial{\partial\phi}+{\overrightarrow a}z\frac\partial{\partial z} \nabla={\overrightarrow a}_{\rho}\frac\partial{\partial\rho}+{\overrightarrow a}_{\phi}\frac1\rho\frac\partial{\partial\phi}+{\overrightarrow a}_z\frac\partial{\partial z}So this is our required result.
Can you try the same result starting from, x=\rho\cos\phi\;;\;y=\rho\sin\phi.
Do not forget to check our Awesome GATE courses.