Block Diagrams and SFG Set-1

[1991: 2M] The signal flow graph of figure shown below, has _______forward paths and ______feedback loops.

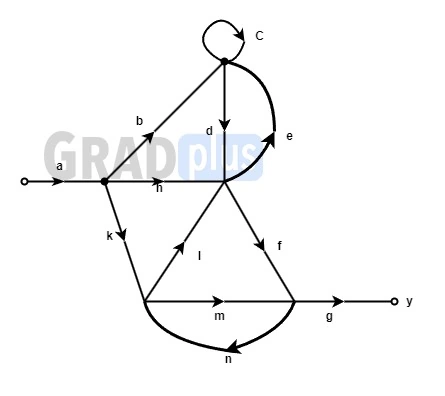
Explanation: From the given signal flow graph, we get

Number of forward paths = 4 (abdfg, ahfg, aklfg, akmg)

Number of loops = 4 (c, de, Ifn, mn)

Therefore , it has 4 forward path and 4 number of loops.

---

[1992: 1 M] The overall transfer function of the system shown in figure is

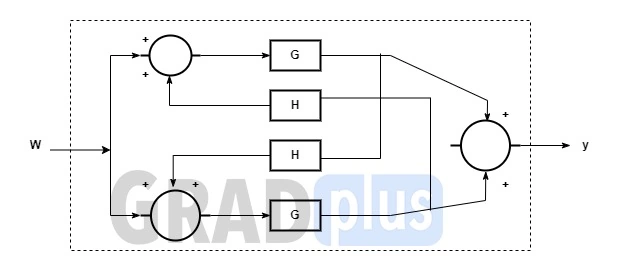
a) \frac G{1-GH}

b) \frac{2G}{1-GH}

c) \frac{GH}{1-GH}

d) \frac{GH}{1-H}

Ans: (b)

Explanation: AS the given block diagram is,

So, from the SFG can be drawn as,

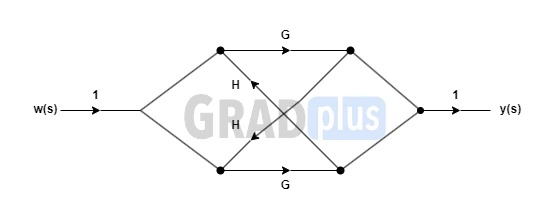
The transfer function is given by,

∴ T.F.=\frac{G+GHG+G+GHG}{1-\lbrack GHGH\rbrack} ….. (4 Forward paths are there)

= \frac{2G}{1-GH}

Therefore, option (b) is the correct answer.

---

[1993: 1 M] Signal flow graph is used to obtain the

a) Stability of a system

b) transfer function of a system

c) controllability of a system

d) observability of a system

Ans: (b)

Explanation:

Signal flow graph is used to find the transfer function between the out put and input node.

Signal flow graph is a graphical representation of a system that shows the flow of signals through the system.

It is a useful tool for analyzing and designing systems in various fields such as electrical engineering, control systems, and communication systems.

So, option (b) is the correct answer.

---

[1995: 1 M] The closed loop transfer function of a control system is given by

\frac{C\left(s\right)}{R\left(s\right)}=\frac{2\left(s-1\right)}{\left(s+2\right)\left(s+1\right)}

For a unit step input the output is

a) -3e^-2t + 4e^-t – 1

b) -3e^-2t -4e^-t + 1

c) zero

d) infinity

Ans: (a)

Explanation: It is given that,

\frac{C\left(s\right)}{1/s}=\frac{2\left(s-1\right)}{\left(s+2\right)\left(s+1\right)} C\left(s\right)=\frac{-1}s+\frac{-3}{s+2}+\frac4{s+1}

∴ C(t)= -1-3e^-2t +4e^-t

For the unit step input, the output is , -1-3e^-2t +4e^-t.

Option (a) is the correct answer.

---

[1998: 2 M]For block diagram shown in figure C(s)/R(s) is given by

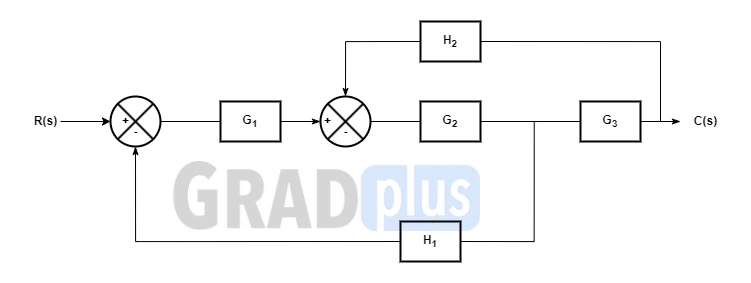
a) \frac{G_1G_2G_3}{1+H_2G_2G_3+H_1G_1G_2}

b) \frac{G_1G_2G_3}{1+G_1G_2G_3+H_1H_2}

c) \frac{G_1G_2G_3}{1+G_1G_2G_3H_1+G_1G_2G_3H_1H_2}

d) \frac{G_1G_2G_3}{1+G_1G_2G_3H_1}

Ans: (a)

Explanation: Give block diagram is,

From the diagrams,

Number of forward paths

= 1(G₁G₂G₃)

Number of loops

= 2 (-G₁G₂H₁, – G₂G₃H₂)

Number of non-touching loops = 0

T.F. = =\frac{C\left(s\right)}{R\left(s\right)}=\frac{G_1G_2G_3}{1+H_1G_1G_2+H_2G_2G_3}

Therefore, option (a) is the correct answer.

---

[2000: 1 M] A linear time invariant system initially at rest, when subjected to a unit step input, gives a response y(t)=te^-t, t > 0. The transfer function of the system is

a) \frac1{\left(s+1\right)^2}

b) \frac1{s\left(s+1\right)^2}

c) \frac1{\left(s+1\right)^2}

d) \frac1{s\left(s+1\right)}

Ans: (c)

Explanation:

X(s) = Lu(t)= \frac1s

Y(s) = L te^-t = \frac1{\left(s+1\right)^2}

∴ T.F. = \frac{Y\left(s\right)}{X\left(s\right)}=\frac s{\left(s+1\right)^2}

Option (c) is the correct answer.

---

[2002: 2 M] The transfer function of the system described by \frac{d^2Y}{dt^2}+\frac{dy}{dt}=\frac{du}{dt}+2u with u as input and y as output is

a) \frac{\left(s+2\right)}{\left(s^2+s\right)}

b) \frac{\left(s+1\right)}{\left(s^2+s\right)}

c) \frac2{\left(s^2+s\right)}

d) \frac2{\left(s^2+s\right)}

Ans: (c)

Expalanation: Given that,

\frac{d^2Y}{dt^2}+\frac{dy}{dt}=\frac{du}{dt}+2u

⇒ s²Y(s) + sY(s) = sU(s) + 2U(s)

\therefore\frac{Y\left(s\right)}{U\left(s\right)}=\frac{s+2}{\left(s^2+s\right)}

Option (c) is the correct answer.

---

[2003: 1 M] A control system is defined by the following mathematical relationship

\frac{d^2x}{dt^2}+6\frac{dx}{dt}+5x=12\left(1-e^{-2t}\right)

The response of the system as t \Rightarrow \infty is

a) x = 6

b) x = 2

c) x = 2.4

d) x = -2

Ans: (c)

Explanation: It is given that ,

\frac{d^2x}{dt^2}+6\frac{dx}{dt}+5x=12\left(1-e^{-2t}\right)

Taking (LT) on the sides

(s + 6s+5)X(s)= 12 \left(\frac1s-\frac1{s+2}\right)

= \frac{24}{s\left(s+2\right)}

X(s)= \frac{24}{s\left(s+2\right)\left(s+1\right)\left(s+5\right)}

Response at t \Rightarrow \infty

Using final value theorem

\underset{t\rightarrow\infty}{Lt}x(t)=\underset{s\rightarrow0}{Lt}sX\left(s\right)

= \underset{s\rightarrow0}{Lt}\frac{s\times24}{s\left(s+1\right)\left(s+2\right)\left(s+5\right)}

Option (c) is the correct answer.

---

[2003: 2 M] A control system with certain excitation is governed by tthe following mathematical equation \frac{d^{2}x}{dt^{2}}+\frac{1}{2}\frac{dx}{dt}+\frac{1}{18}x=10+5e^{-4t}+2e^{-5t} The natural time constant of the response of system are

a) 2s and 5s

b) 3s and 6s

c) 4s and 5s

d) 1/3s and 1/6s

Ans: (b)

Explanation: Given equation is, \frac{d^{2}x}{dt^{2}}+\frac{1}{2}\frac{dx}{dt}+\frac{1}{18}x=10+5e^{-4t}+2e^{-5t}. The given differential equation is a second order linear homogenous equation .

We know that, Natural time constant of the response depends only on poles of the system.

T(s)= \frac1{s^2+s/2+1/18}

\frac{18}{18s^2+9s+1} \frac{18}{\left(6s+1\right)\left(3s+1\right)}

This is in the form\frac1{\left(1+sT_1\right)\left(1+sT_2\right)}

∴ T₁, T₂ = 6 sec, 3 sec.

Option (b) is the correct answer.

---

[2003: 2 M] The block diagram of a control system is Shown in figure. The transfer function G(s) = Y(s)/U(s) of the system is

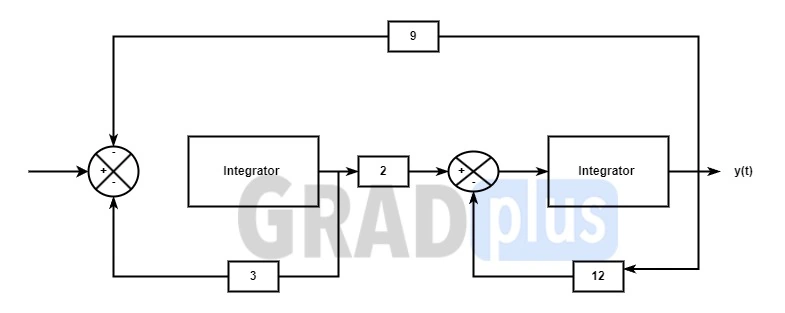
a) \frac1{18\left(1+{\displaystyle\frac s{12}}\right)\left(1+{\displaystyle\frac s3}\right)}

b) \frac1{27\left(1+{\displaystyle\frac s6}\right)\left(1+{\displaystyle\frac s9}\right)}

c) \frac1{27\left(1+{\displaystyle\frac s{12}}\right)\left(1+{\displaystyle\frac s9}\right)}

d) \frac1{27\left(1+{\displaystyle\frac s9}\right)\left(1+{\displaystyle\frac s3}\right)}

Ans: (b)

Explanation:

As it is said that the Integrator are represemnted as 1/s in s-domain , so the diagram becomes,

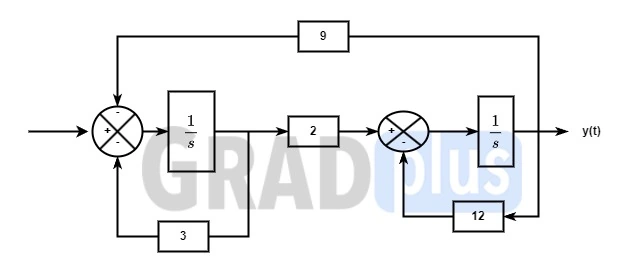
As per the block diagram, the corresponding signal flow graph is drawn

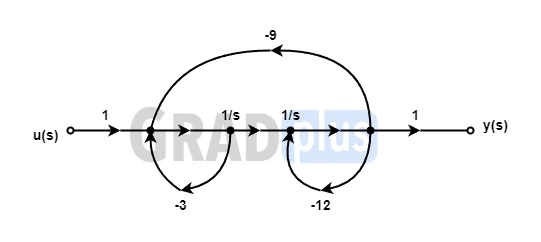
One forward path P₁ = 2/s²

The individual loops are,

L_1=-\frac3s,\;L_2=-\frac{12}sand\;L_3=-\frac{18}{s^2}

From the signal flow graph, we can see that , there is one forward path, and two non-touching loops.

L₁ and L₂ are non-touching loops

L₁L₂= \frac{36}{s^2}

The loops touches the forward Path ∆₁ = 1

The graph determinant is

∆ 1 -(L₁ + L₂ + L₃)+ L₁L₂

= =1+\frac3s+\frac{12}s+\frac{18}{s^2}+\frac{36}{s^2}

Applying Mason,s gain formula ,

G(s)= \frac{Y(s)}{U(s)}=\frac{P_1\triangle_1}\triangle

= \frac2{s^2+15s+54} \frac2{\left(s+9\right)\left(s+6\right)} \frac1{27\left(1+{\displaystyle\frac s9}\right)\left(1+{\displaystyle\frac s6}\right)}

Therefore, option (b) is the correct answer.

---