Next Lesson

Basics Set-1

5 (B) Control Systems Topic-wise Previous Solved GATE Papers Basics Set-1

[1994 : 1 Mark] Tachometer feedback in a DC position control system enhances stability (T/F)

Ans. True

Explanation :

WE know that, The tachometer feedback is a derivative feedback. So, tachometer adds zero at origin.

Hence, type decreases and stability is improved (True).

Therefore, the given statement is a true statement.

[1995 : 1 Mark] The transfer function of a linear system is the

(a) Ratio of the output, V₀(t) and input V_i(t)

(b) Ratio of the derivatives of the output and the input

(d) None of these

Answer : (c)

Explanation :

In general, we know thatThe transfer function of a linear time invariant system is defined as the ratio of the Laplace transform of the output and that of the input with all initial conditions zero.

So, option (c) is the correct answer.

[1998 : 1 Mark] The transfer function of a tachometer is of the form

(a) Ks

(b) $\frac{K}{s}$

(d) $\frac{K}{s(s+1)}$

Answer : (a)

Explanation :

In general, Tachometer is basically a differentiator. So, the transfer function of a tachometer is of the form Ks.

So, option (a) is the correct answer.

[2001 : 2 Marks] An electrical system and its signal-flow graph representations are shown in the figure (a) and (b) respectively. The values of G₂ and H respectively are

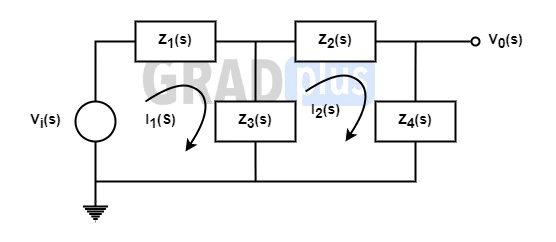
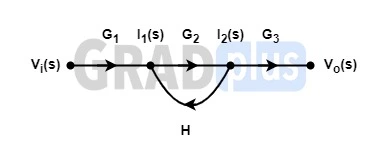
(a) $\frac{Z_3(s)}{Z_2(s)+Z_3(s)+Z_4(s)},\frac{-Z_3(s)}{Z_1(s)+Z_3(s)}$

(b) $\frac{-Z_3(s)}{Z_2(s)-Z_3(s)+Z_4(s)},\frac{-Z_3(s)}{Z_1(s)+Z_3(s)}$

(d) $\frac{-Z_3(s)}{Z_2(s)-Z_3(s)+Z_4(s)},\frac{Z_3(s)}{Z_1(s)+Z_3(s)}$

Answer : (c)

Explanation : The given signal-flow graph is,

Now, let us apply KVL in both loops, In the fig.a)

In first loop,

V_i(s)=I_1(s)Z_1(s)+\left[I_1(s)-I_2(s) \right ]Z_3(s)

V_i(s)=I_1(s)\left[Z_1(s)+Z_3(s) \right ]-I_2(s)Z_3(s)

$\frac{V_i(s)}{Z_1(s)+Z_3(s)}=I_1(s)-\frac{I_2(s).Z_3(s)}{Z_1(s)+Z_3(s)}$ —– (i)

In Second Loop,

\left[I_2(s)-I_1(s) \right ]Z_3(s)+I_2(s)Z_2(s)+I_2(s)Z_4(s)=0

I_2(s)\left[Z_2(s)+Z_3(s)+Z_4(s) \right ]=I_1(s).Z_3(s)

G_2=\frac{I_2(s)}{I_1(s)}=\frac{Z_3(s)}{Z_2(s)+Z_3(s)+Z_4(s)}

From the SFG, $I_1(s)=V_iG_1(s)+I_2(s)H(s)$

$I_1(s)=V_i(s)\frac{1}{Z_1(S)+Z_3(s)}+I_2(s)\frac{Z_3(s)}{Z_1(s)+Z_3(s)}$ —– From (i)

$\therefore H(s)=\frac{Z_3(s)}{Z_1(s)+Z_3(s)}$ —–(Comparing above two equations)

The value of G2 is $G_2=\frac{I_2(s)}{I_1(s)}=\frac{Z_3(s)}{Z_2(s)+Z_3(s)+Z_4(s)}$ and value of H $\therefore H(s)=\frac{Z_3(s)}{Z_1(s)+Z_3(s)}$

So, option (c) is the correct answer.

[2001 : 2 Marks] The open-loop DC gain of a unity negative feedback system with closed-loop transfer function $\frac{s+4}{s^2+7s+13}$ is

(a) $\frac{4}{13}$

(b) $\frac{4}{9}$

(d) 13

Answer : (b)

Explanation : We know, that the closed lop transfer function (CLSF) is given by,

CLTF=\frac{G(s)}{1+G(s)H(s)}=\frac{s+4}{s^2+7s+13}

\frac{1+G(s)H(s)}{G(s)}=\frac{s^2+7s+13}{s+4}

H(s) = 1 for unity feedback

\frac{1}{G(s)}=\frac{s^2+7s+13}{s+4}-1

\frac{1}{G(s)}=\frac{s^2+6s+9}{s+4}

{G(s)}=\frac{s+4}{s^2+6s+9}

For DC s = 0

G(s) = Open loop gain

{G(s)}=\frac{4}{9}

So, option (b) is the correct answer.

[2004 : 2 Marks ] A system described by the following differential equation $\frac{d^2y}{dy^2}+3\frac{dy}{dt}+2y=x(t)$ is initially at rest. For input x(t) = 2u(t), the output y(t) is

(a) $(1-2e^{-t}+e^{-2t})u(t)$

(b) $(1+2e^{-t}-e^{-2t})u(t)$

(d) $(0.5+2e^{-t}+2e^{-2t})u(t)$

Answer : (a)

Explanation : It is given that,

\frac{d^2y}{dt^2}+\frac{3dy}{dt}+2y=X(t)

s^2Y(s)+3sY(s)+2Y(s)=X(s)

x(t) = 2 u(t)

X(s)=\frac{2}{s}

\therefore (s^2+3s+2)Y(s)=\frac{2}{s}

Y(s)=\frac{2}{s(s+2)(s+1)}

\frac{2}{s(s+2)(s+1)}=\frac{A}{s}+\frac{B}{s+2}+\frac{C}{s+1}

2 = A(s + 2)(s + 1)+ B s(s + 1)+ C(s + 2 )s

s = 0, 2 = 2A ⇒ A = 1

s = -1, 2 = -C ⇒ C = -2

s = -2, 2 = 2B ⇒ B = 1

Y(s)=\frac{1}{s}+\frac{1}{s+2}-\frac{2}{s+1}

y(t)=\left[1+e^(-2t)-2e^(-t) \right ]u(t)

The output y(t) is $(1-2e^{-t}+e^{-2t})u(t)$ .

Therefore, option (a) is the correct answer.

[2005 : 1 Mark] Despite the presence of negative feedback, control systems still have problems of instability because the

(a) Components used have non linearities

(b) Dynamic equations of the systems are not known exactly

(d) Systems has large negative phase angle at high frequencies

Answer : (d)

Explanation :- In general, the negative feedback reduces the overall gain and increases stability. It improves bandwidth and input and output impedances . It reduces the sensitivity of output to input variation, distortion and noise reduction.

So, option (d) is the correct answer.

[2006 : 1 Mark] In the system shown below, x(t) = (sin t)u(t). In steady-state, the response y(t) will be

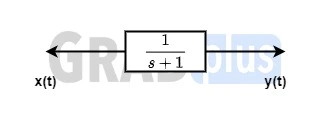
(a) $\frac{1}{\sqrt{2}}sin\left(t-\frac{\pi}{4} \right )$

(b) $\frac{1}{\sqrt{2}}sin\left(t+\frac{\pi}{4} \right )$

(d) $sin(t)-cos(t)$

Answer : (a)

Explanation : It is given that,

y(t) = x(t) * h(t)

Now, taking the laplace transformation,

Y(s) = X(s) . H(s)

H(j\omega )=\frac{1}{s+1}=\frac{1}{\sqrt{2}}\angle -45^{\circ}

H(j\omega )=\frac{1}{\sqrt{2}}\;\angle -\frac{\pi}{4}

x(t) = sin(t)u(t)

\therefore y(t)=\frac{1}{\sqrt{2}}sin\left(t-\frac{\pi}{4} \right )

Option (a) is he correct answer.

[2006 : 2 Marks] The unit-step response of a system starting from rest is given by

c(t)=1-e^{-2t}\;\;\;for\;t\geq0

The transfer function of the system is

(a) $\frac{1}{1+2s}$

(b) $\frac{2}{2+s}$

(d) $\frac{2s}{1+2s}$

Answer : (b)

Explanation : Given that,

c(t)=1-e^{-2t}\;\;\;for\;t\geq0

Now, taking the laplace transform,

C(s)=\frac{1}{s}-\frac{1}{s+2}=\frac{2}{s(s+2)}

R(s)=\frac{1}{s}

H(s)=\frac{C(s)}{R(s)}=\frac{2}{s+2}

Therefore, the transfer function of the system is $H(s)=\frac{C(s)}{R(s)}=\frac{2}{s+2}$

Therefore, option (b) is the correct answer.

[2006 : 2 Marks] The unit impulse response of a system is h(t) = e^-t , t ≥ 0

For this system, the steady-state value of the output for unit step input is equal to

(a) -1

(b) 0

(d) ∞

Answer : (c)

Explanation : Given that,

h(t)=e^{-t}

Now, taking laplace transform of the given function,

H(s)=\frac{1}{s+1}

R(s)=\frac{1}{s}

Output = $H(s)R(s)=\frac{1}{s+1}\frac{1}{s}$

\frac{1}{s(s+1)}=\frac{A}{s}+\frac{B}{s+1}

1 = A (s+1) + Bs

s = 0, 1 = A

s = -1, 1 = -B

\therefore Output =\frac{1}{s}-\frac{1}{s+1}

= (1 – e^-t) u(t)

When t = ∞ at steady state

Output = 1

So, option (c) is the correct answer.

Back to Course

Next Lesson