Why E and H are mutually perpendicular, in the EM wave?

In the Electromagnetic Wave, we have E i.e. Electric Field and H i.e. Magnetic Field lying mutually perpendicular. Let’s see why this is so, in a broader way.

What is Electromagnetic Wave?

Electromagnetic wave is a systematic movement of varying E and varying H, which transports energy from one location to the other.

The existanance of an EM wave is evident by the Maxwell’s equations. Using Maxwell’s equations we can prove that electromagnetic energy can be transported from one point in the space to other.

You can watch the quick video below or read along.

How E and H are mutually perpendicular within EM wave

We know that EM wave is a biproduct of Maxwell’s equations. For free space Maxwell’s equations are written as follows.

\nabla\times\overrightarrow H=\varepsilon_0\frac{\partial\overrightarrow E}{\partial t} \nabla\times\overrightarrow E=-\mu_0\frac{\partial\overrightarrow H}{\partial t} \nabla\cdot\overrightarrow E=0 \nabla\cdot\overrightarrow H=0

Consider very first equation,

\nabla\times\overrightarrow H=\varepsilon_0\frac{\partial\overrightarrow E}{\partial t}

This equation indicate us that, at any point in the space, time varying E and H are co-exists, isn’t it?

Let us assume at a point in the space, time varying E is present.

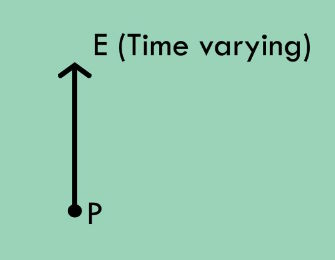
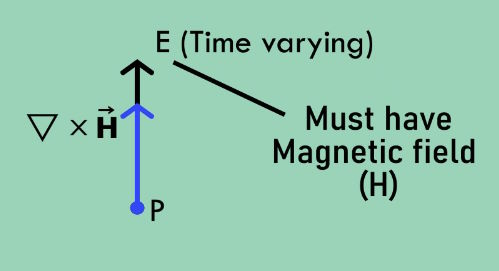
Then, this equation \nabla\times\overrightarrow H=\varepsilon_0\frac{\partial\overrightarrow E}{\partial t} tells us that, at that same point, magnetic field must also present such that its curl aligning with E.

Now we know the curl operation, it gives maximum circulation of the vector field and the curl vector is perpendicular to the plane of vector field.

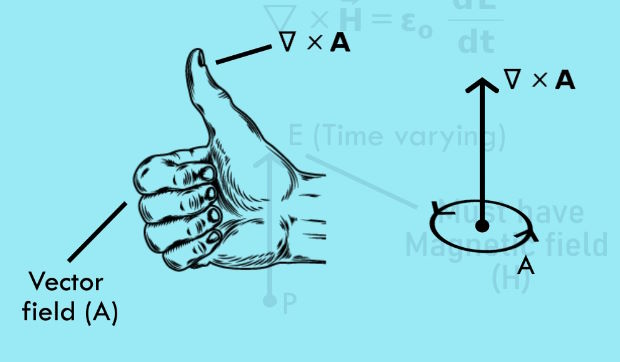
Hence, in our case if \nabla\times\overrightarrow H is along E, then H must be along the plane perpendicular to E.

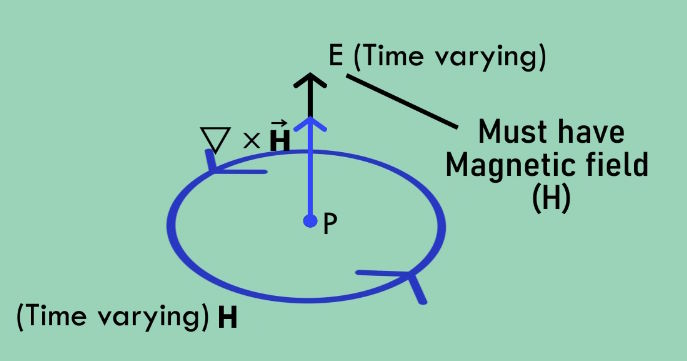
Similarly, if you consider \nabla\times\overrightarrow E=-\mu_0\frac{\partial\overrightarrow H}{\partial t}, you will get the same result.

So, in a broader way, you can remember that E and H have to be mutually perpendicular due to that fact that they are connected by the curl operation. SImple!