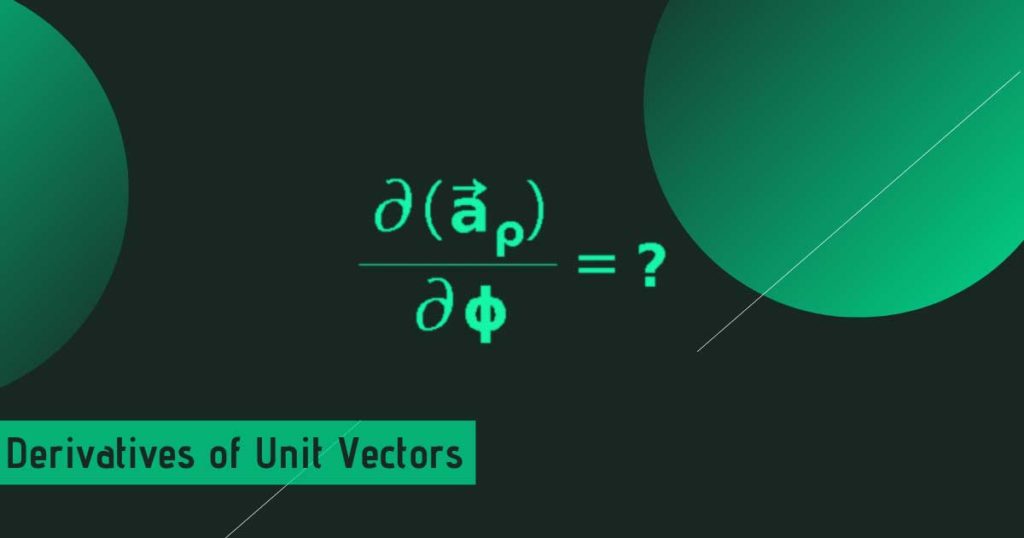
Each coordinate system is uniquely represented with a set of unit vectors. You may think them as the constants and their derivatives be zero. But derivatives of the unit vectors are not zero all the time. This article discusses the same in detail for each coordinate system
Derivatives of Cartesian Unit Vectors
In Cartesian Coordinate System, any point is represented using three coordinates i.e. x, y and z. The x-coordinate is the perpendicular distance from the YZ plane. The y-coordinate is the perpendicular distance from the XZ plane, similarly, z-coordinate is the normal distance from XY plane.
In this coordinate system, any vector is represented as follows
\overrightarrow A=A_x{\overrightarrow a}_x+A_y{\overrightarrow a}_y+A_z{\overrightarrow a}_zAx is the x-component, Ay is the y-component and Az is the z-component of given vector. Component of the vector along any axis is a flux or effect of the given vector along that axis.
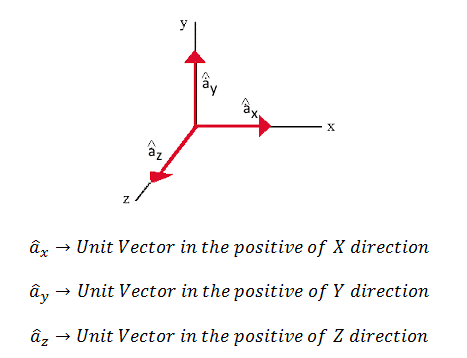
So these are the unit vectors in the Cartesian Coordinate System. Any unit vector has a constant magnitude i.e. unity and direction along specific axis.
Consider for example ax having unit magnitude and in the direction of positive X axis. Now, let us say you are moving in X direction i.e. change is along X. Whatever be your change dx, the nature of ax i.e. its magnitude and direction is going to be same. In other words, the rate of change of ax w.r.t. dx is zero.
\frac\partial{\partial x}{\overrightarrow a}_x=0The same logic can be extended for the change along Y and Z. For any dy and dz, the nature of ax is constant. And hence,
\frac\partial{\partial y}{\overrightarrow a}_x=0\;\;\;\;\;and\;\;\;\;\frac\partial{\partial z}{\overrightarrow a}_x=0So ax is a global constant i.e. neither its magnitude nor its direction is changing with any space change (dx, dy or dz) at any point in the space. Same is the story with ay and az. So we have,
\frac\partial{\partial x}{\overrightarrow a}_y=0;\;\frac\partial{\partial y}{\overrightarrow a}_y=0;\;\frac\partial{\partial z}{\overrightarrow a}_y=0 \frac\partial{\partial x}{\overrightarrow a}_z=0;\;\frac\partial{\partial y}{\overrightarrow a}_z=0;\;\frac\partial{\partial z}{\overrightarrow a}_z=0Derivatives of Cylindrical Unit Vectors
In Cylindrical Coordinate system, any point is represented using ρ, φ and z.
ρ is the radius of the cylinder passing through P or the radial distance from the z-axis. φ is called as the azimuthal angle which is angle made by the half-plane containing the required point with the positive X-axis. The anticlockwise direction of rotation i.e. from the +X axis to +Y axis is considered as a positive angle. z coordinate is the same as in the Cartesian system; it is the distance of the required point from the XY plane.
Any vector in a Cylindrical coordinate system is represented using three mutually perpendicular unit vectors as shown.
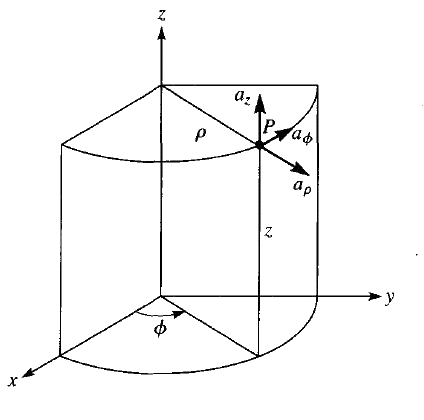
Consider point P and unit vector {\overrightarrow a}_\rho at that point. {\overrightarrow a}_\rho has magnitude unity and the direction along increasing radial distance. Now let us say we are finding the change in aρ with respect to ρ i.e. dρ.
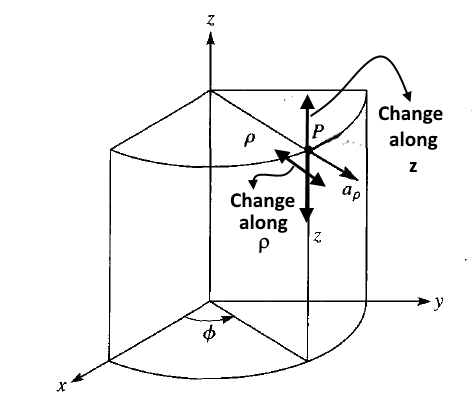
Now as you can observe from the figure, the aρ is remaining constant for any change along ρ. In other words neither the magnitude nor the direction of the aρ is changing w.r.t. change in ρ. So its derivative with respect to dρ is zero. The same explanation is valid for the change in aρ with respect to z.
\frac\partial{\partial\rho}{\overrightarrow a}_\rho=0\;\;and\;\;\;\frac\partial{\partial z}{\overrightarrow a}_\rho=0Now, consider the change in aρ with respect to phi i.e. d(aρ)/dφ. Let us say, for the dφ i.e. change along φ, we are moving from φ1 at P to φ2 at Q, as shown in the figure.
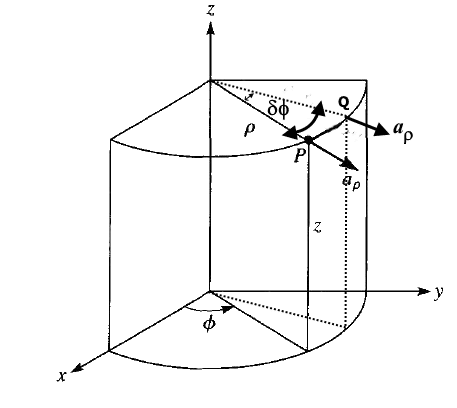
As you can observe from the figure, the direction of aρ at P and Q are different. That means with change in phi the direction of aρ also changes. Keep in mind that aρ and aφ are defined at the given point. So as the point changes their direction changes. So in other words d(aρ)/dφ will not be zero for sure. So how to calculate it?
For getting this derivative let us transform aρ into the equivalent cartesian coordinate system. The logic behind this is very simple. The Cartesian unit vectors are globally constant hence it would be easy for the derivation process. We know that,
{\overrightarrow a}_\rho=\cos\phi\;{\overrightarrow a}_x+\sin\phi\;{\overrightarrow a}_y \therefore\frac\partial{\partial\phi}\left({\overrightarrow a}_\rho\right)={\overrightarrow a}_x\frac\partial{\partial\phi}\cos\phi\;+{\overrightarrow a}_y\frac\partial{\partial\phi}\sin\phi=-\sin\phi{\overrightarrow a}_x+\cos\phi{\overrightarrow a}_y But,\;a_\phi=-\sin\phi{\overrightarrow a}_x+\cos\phi{\overrightarrow a}_y \therefore\frac\partial{\partial\phi}\left({\overrightarrow a}_\rho\right)={\overrightarrow a}_\phiAlso, all the derivatives of the az are zero. As explained in the Cartesian section above, az is global type of constant and hence its change will be zero irrespective of the variable of differentiation.
\frac\partial{\partial\rho}{\overrightarrow a}_z=0;\;\frac\partial{\partial\phi}{\overrightarrow a}_z\;=0;\;\frac\partial{\partial z}{\overrightarrow a}_z=0Similarly, the change of aφ with respect to ρ and z will be zero due to the fact that the incremental change along ρ or z doesn’t affect the aφ. So,
\frac\partial{\partial\rho}\left({\overrightarrow a}_\phi\right)=\frac\partial{\partial z}\left({\overrightarrow a}_\phi\right)=0But again as seen from the diagram below, the direction of aφ changes with change in φ.
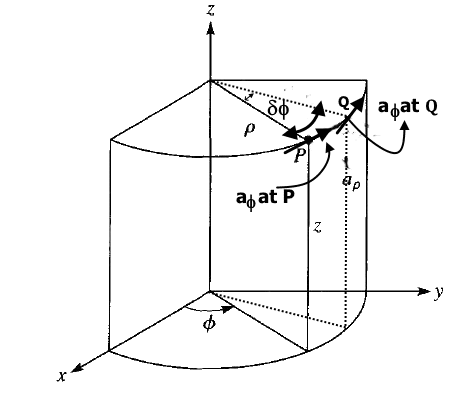
So again following the similar step as above, we have,
\frac\partial{\partial\phi}\left({\overrightarrow a}_\phi\right)=\frac\partial{\partial\phi}\left(-\sin\phi{\overrightarrow a}_x+\cos\phi{\overrightarrow a}_y\right)=-\cos\phi{\overrightarrow a}_x-\sin\phi{\overrightarrow a}_y \therefore\frac\partial{\partial\phi}\left({\overrightarrow a}_\phi\right)=-\left(\cos\phi{\overrightarrow a}_x+\sin\phi{\overrightarrow a}_y\right)=-{\overrightarrow a}_\rhoSo we can summarize the derivatives of the Cylindrical unit vectors as follows:
\frac\partial{\partial\rho}\left({\overrightarrow a}_\rho\right)\;=0;\;\frac\partial{\partial\rho}\left({\overrightarrow a}_\phi\right)=0;\;\frac\partial{\partial\rho}\left({\overrightarrow a}_z\right)=0 \frac\partial{\partial\phi}\left({\overrightarrow a}_\rho\right)\;={\overrightarrow a}_\phi;\;\frac\partial{\partial\phi}\left({\overrightarrow a}_\phi\right)=-{\overrightarrow a}_\rho;\;\frac\partial{\partial\phi}\left({\overrightarrow a}_z\right)=0 \frac\partial{\partial z}\left({\overrightarrow a}_\rho\right)\;=0;\;\frac\partial{\partial z}\left({\overrightarrow a}_\phi\right)=0;\;\frac\partial{\partial z}\left({\overrightarrow a}_z\right)=0Derivatives of Spherical Unit Vectors
Same logic can be thought for the deriving the spherical unit vectors. We can follow the similar steps and conclude to following results.
\frac\partial{\partial r}\left({\overrightarrow a}_r\right)=0;\;\frac\partial{\partial\theta}\left({\overrightarrow a}_r\right)={\overrightarrow a}_\theta;\;\frac\partial{\partial\phi}\left({\overrightarrow a}_r\right)=\sin\theta{\overrightarrow a}_\phi \frac\partial{\partial r}\left({\overrightarrow a}_\theta\right)=0;\;\frac\partial{\partial\theta}\left({\overrightarrow a}_\theta\right)=-{\overrightarrow a}_r;\;\frac\partial{\partial\phi}\left({\overrightarrow a}_\theta\right)=\cos\theta{\overrightarrow a}_\phi \frac\partial{\partial r}\left({\overrightarrow a}_\phi\right)=0;\;\frac\partial{\partial\theta}\left({\overrightarrow a}_\phi\right)=0;\;\frac\partial{\partial\phi}\left({\overrightarrow a}_\phi\right)=-({\overrightarrow a}_r\sin\theta+{\overrightarrow a}_\theta\cos\theta)Conclusion
We may consider the unit vectors as constants and their derivatives are zero. But this is not true all the time. The Cartesian unit vectors are universal ones and their derivatives are always zero. But Cylindrical and Spherical unit vector are location dependent unit vectors and their derivatives may be zero or may not be zero.
Keep Learning! Keep Going!
Do not forget to check our Awesome GATE courses.