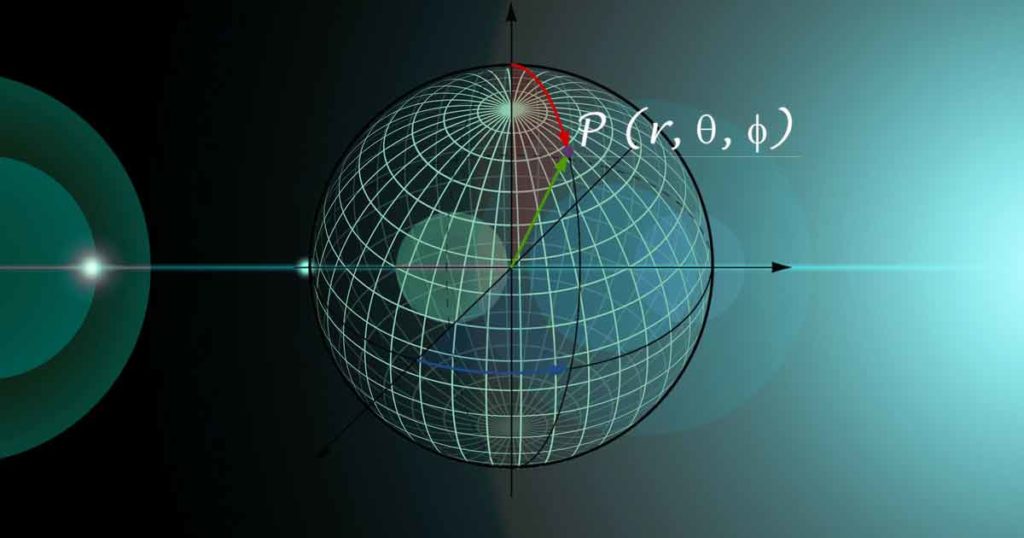
Spherical Coordinate System is widely used in Engineering and Science studies. In this article, let us revive it from the point of view of Electromagnetics.
In Electromagnetic Fields, we mainly use Cartesian, Cylindrical and Spherical Coordinate Systems. The Spherical symmetry is evident in many cases of Electromagnetics like field due to point charge, radiation pattern of antenna etc.
What are Spherical Coordinates?
P (r, θ, φ)
r is the distance of point P from origin or radius of hypothetical sphere at origin passing through point P.
θ aka colatitude, is the minimum angle between position vector or ‘r’ of the given point and positive Z-axis.
φ is same as in cylindrical coordinate system; angle made by the half plane containing the required point with the positive X-axis.
The Spherical Frame of Reference
r coordinate
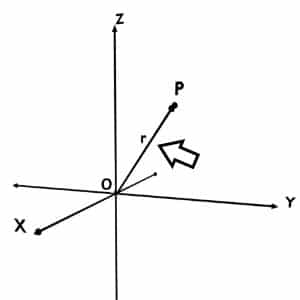
Consider that P is any point in the space. Assume the coordinate axis is same as the cartesian or cylindrical coordinate system as the reference.
Then the distance of this point P from the origin is considered as the r coordinate.
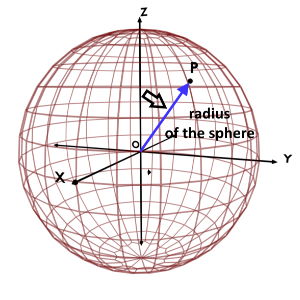
r coordinate is also defined as the radius of the imaginary sphere centered at the origin and passing through the given point.
Range of ‘r’ coordinate
r coordinate of the Spherical Coordinate System can take any value from 0 to ∞. Points can be present anywhere in the space. And r coordinate of any point is the distance from Origin.
For example, consider two points P and Q whose r coordinates are shown in the figure.
So obviously, at the maximum, point can be at infinity. And at the minimum, point can be itself an origin with ZERO distance.
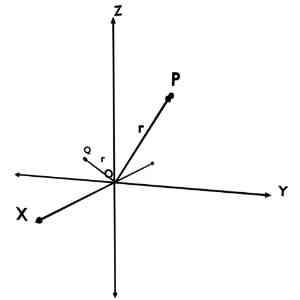
Note that, r coordinate can never be negative because it’s a distance of the given point from the Origin. There is not positive or negative side as we have seen in Cartesian Coordinates. Actually, it’s a radius of the imaginary Sphere passing through the given point. And it can never be negative.
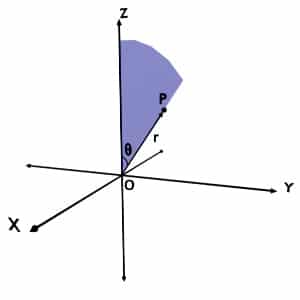
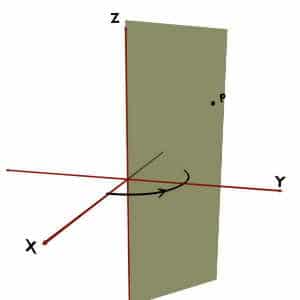
Theta (θ) coordinate
It is the minimum angle between the radius r or the position vector of the given point with the +Z-axis.
Again consider any point P in the space. So the minimum angle made by OP vector with +Z axis, as shown in figure, is theta coordinate of P.
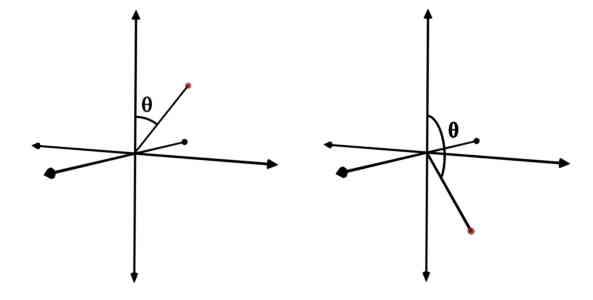
Now, let us consider the same point P, but trace the angle between r and +Z in the direction as shown in figure.
Note that, this angle is also the angle between position vector of the point and +Z axis. But it is not the minimum angle between them. So, this cannot be theta.
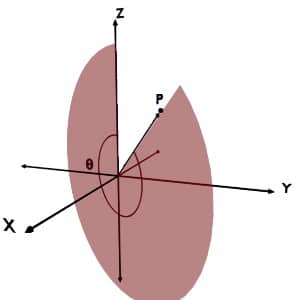
Range of θ coordinate
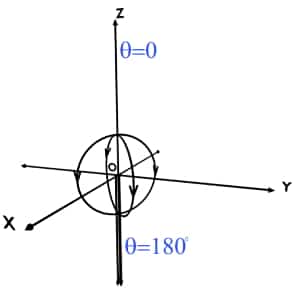
The given point can present anywhere in the space, in any octant. And based on the definition for theta coordinate, it can take any value between 0o to 180o.
Why does Theta of Spherical Coordinate System range from 0 to 180 and not to 360?
Watch: Why does Theta of Spherical Coordinate System range from 0 to 180 and not to 360?
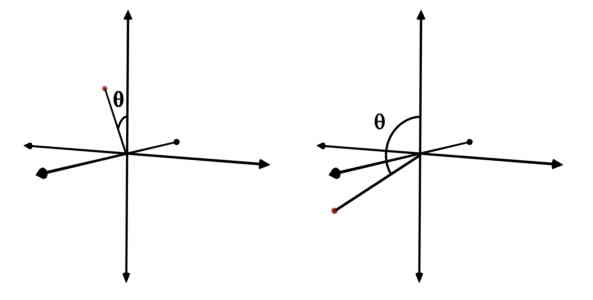
Though theta is an angle, it can take value only up to 180o and not 360o. The reason is quite obvious. It is the minimum angle between the position vector of the point (r) and +Z axis. Let us understand this by following example.
Consider any point P present in the space. The position vector of this point i.e. r forms two angles with +Z axis, based on the nature of tracing, as shown in following figures. But, according to the definition, you should go with the minimum one.
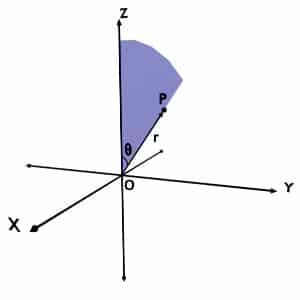
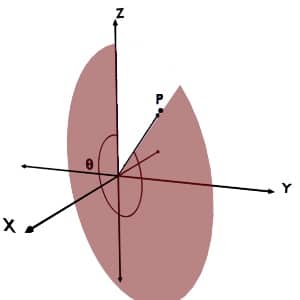
So, for any point around the Z axis, the angle made by the r with +Z axis is always less or equal to 180o.
Also, theta can never be negative.
There is no positive or negative side of tracing theta. It is just the minimum angle between r and +Z axis, all around the Z axis.
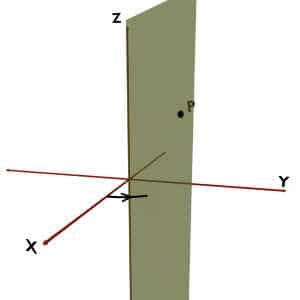
Phi (φ) coordinate
It is same as the φ in the cylindrical coordinate system.
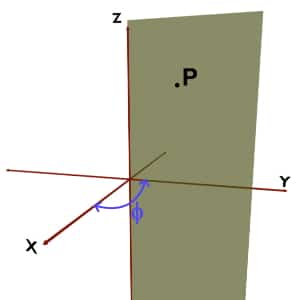
Consider any point P in the space. Imagine that you are constructing a plane stuck to Z axis, so that it would pass through the given point P.Such imaginary plane is called as a vertical half plane.
And angle made by this half plane with the +X-axis is the φ coordinate of the spherical coordinate system.
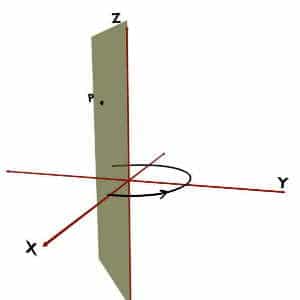
When do we take Phi (ϕ) negative?
Watch: When do we take phi negative in Cylindrical Coordinate System?
Remember that, an angle made by the vertical half plane with the +X axis is the Phi (ϕ) coordinate. But, which way should trace this angle?
For example, consider the point P present in space. Now to define Phi of this point P, we would need vertical half plane. A vertical half plane is an imaginary plane stuck to Z-axis so that it would pass through the given point i.e. P. It is shown by green in the following figures. The angle made by this vertical half plane with the +X axis is the Phi (ϕ) coordinate.
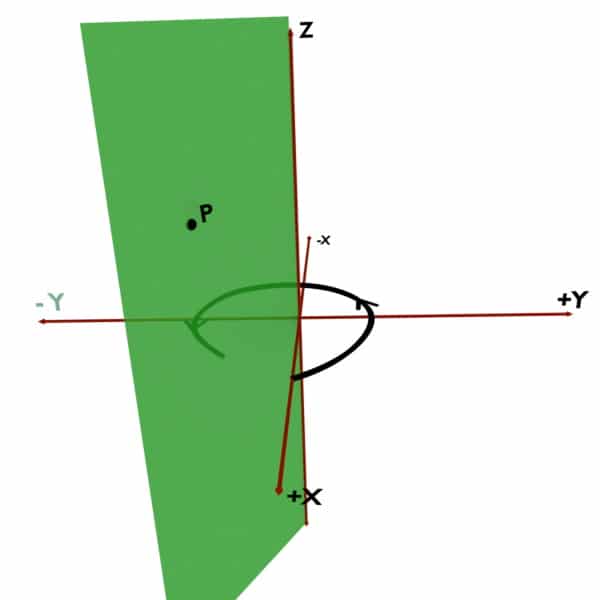
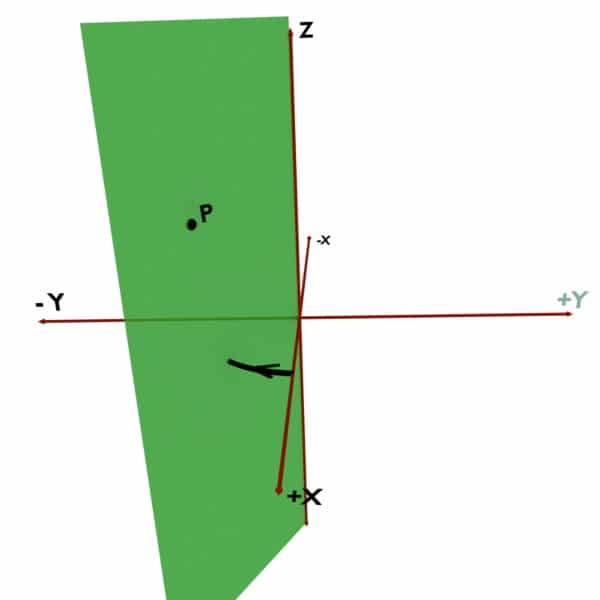
Now the problem is, how should we take this angle? Should we trace it in anticlockwise direction as shown in first diagram? Or should we trace it in clockwise direction as shown in second diagram?
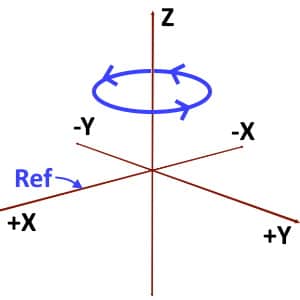
So remember that, according to Cylindrical Coordinate System’s convention, Phi (ϕ) must be traced in Anticlockwise direction. That is, your path of tracing should be along +X to +Y to -X to -Y to +X.
And, if you trace the angle in clockwise direction viz. along +X to -Y to -X to +Y to +X, then you take Phi (ϕ) NEGATIVE.
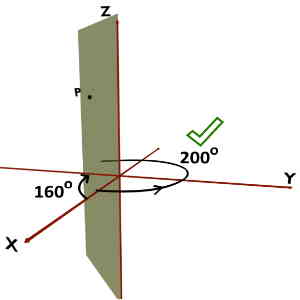
For example, consider a point P and the vertical half plane containing it. This plane makes angle 200o if traced in the anticlockwise direction and 160o if traced in clockwise direction. So, the correct Phi(ϕ) would be 200o or -160o.
Range of Phi (ϕ) coordinate.
Point can be present anywhere in the space. And the vertical half plane stuck to the Z axis, to contain that point, could have any orientation within 360 degrees. Hence, Phi can take any value between 0o to 360o or 0 to 2π.
Constant Coordinate Surfaces
In Cartesian and Cylindrical System, we observed that, locus of any one coordinate as a constant, is a surface or plane. Similar is the case with Spherical Coordinate System. Any one coordinate as a constant while other two variables would lead to a surface or plane.
r = constant Surface
Assume that we are given with r=2 while φ and θ coordinates can take any value.
We are given with r coordinate equal to 2 i.e. r = constant and no restrictions over the value of φ and θ coordinates. So, just apply the definition of r coordinate.
r is the distance of the point from origin. And all the points present on the sphere of radius, r = 2, will be lying at a distance of 2 from the origin. Of course phi and theta coordinates for such points are different. But they all have r coordinate as 2.
Hence, locus of r = 2 is a curved surface of the sphere centered at origin at having radius 2.
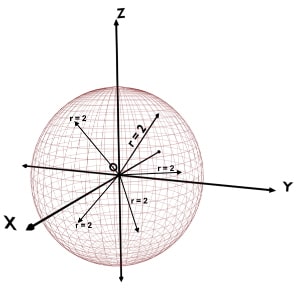
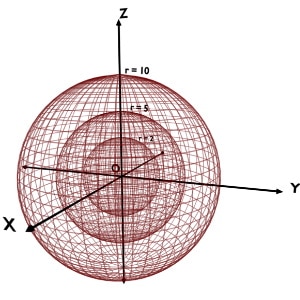
So, the locus of r = constant is a curved surface of the sphere centered at origin with radius equal to that r.
Phi ( φ ) = constant Surface
Assume that, φ is equal to constant while r and θ coordinates can take any value.
As in cylindrical coordinate system, we have seen that locus of φ = constant is a vertical half plane stuck to the Z – axis making an angle φ with the +X axis.
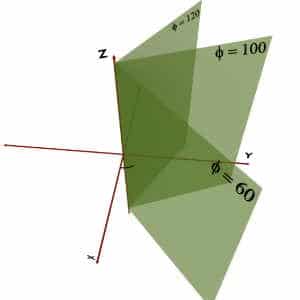
Theta ( θ ) = constant Surface
Case [1] : Assume that we are given with θ, less than 900
Consider θ = 300 while r and φ coordinates can take any value.
We are given with θ equal to 300 i.e. θ = constant and no restrictions over the value of r and φ coordinates.
So, just apply the definition of θ coordinate. It is the minimum angle made by the position vector with +Z axis.
So obviously all the points present on the surface, inverted cone as shown in figure, will have θ =300 .
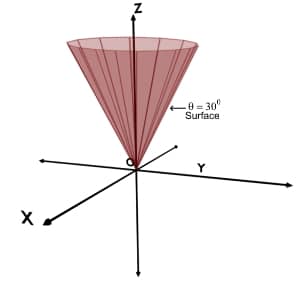
So, the locus of θ = constant (for less than 900) will form a conical curved surface above the XY plane with apex at origin and slant side making angle θ with + Z axis.
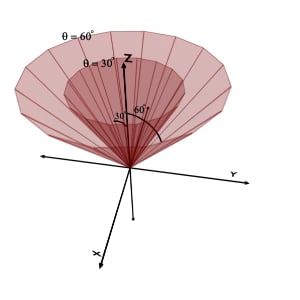
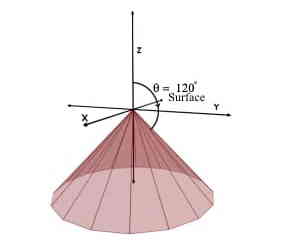
Case [2] : Assume that we are given with θ greater than 900
Consider θ = 1200 while r and φ coordinates can take any value.
We are given with θ equal to 1200 i.e. θ = constant and no restrictions over the value of r and φ coordinates.
Now, the locus of θ greater than 900 will form a conical curved surface below the XY plane with apex at origin and slant side making angle θ with +Z axis.
Case [3] : Assume that we are given with θ equal to 900 while r and φ coordinates can take any value.
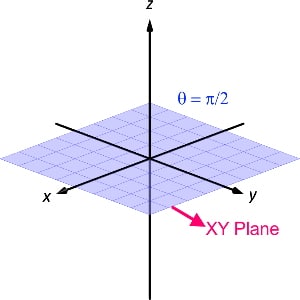
We are given with θ equal to 900 i.e. θ = constant and no restrictions over the value of r and φ coordinates.
So, the locus of θ equal to 900 is exactly same as the XY plane.
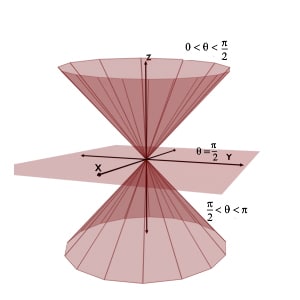
The summarized figure of all the three cases of theta equals to constant, i.e. θ less than 900 , θ equals to 900 and θ greater than 900 are as shown in the figure.
Lines in Spherical Coordinate System
What would be locus if we are given with two coordinates constants and remaining one variable?
Simple! It would be a line.
When a coordinate is constant, it leads to surface. So, when two coordinates are constants then it would lead to two surfaces. And the intersection of these two surfaces/planes would be our required locus i.e. line , as we have seen in cartesian and cylindrical coordinate system.
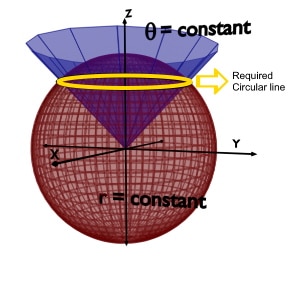
r = constant & phi (φ) = constant
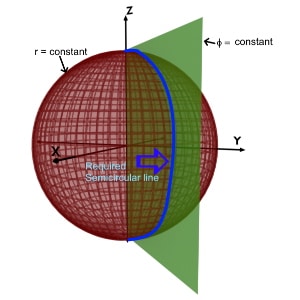
We know that, r=constant is a sphere having radius r. And phi(φ)=constant is a vertical half plane. So the intersection of these two planes is a line along theta (θ).
As theta (θ) is an angle up to 180o, so the line along theta (θ) is nothing but a semicircle or semicircular line.
r = constant and theta (θ) = constant
r=constant is a sphere having radius r and theta(θ)=constant is a conical curved surface.
So the intersection of these two planes is a circle i.e. a line along the phi (φ).
Theta(θ)=constant & Phi(φ)=constant
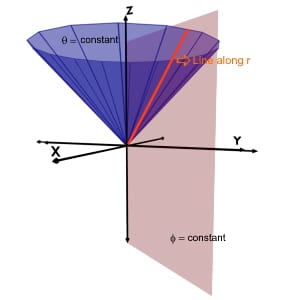
Theta(θ)=constant is a conical curved surface and phi(φ)=constant is a vertical half plane.
So the intersection of these two planes will be a line along radius r.
So remember that, if two coordinates given as constants and remaining one is variable then the locus is a line along the variable coordinate.
Also remember that, if range of the variable coordinate is not given then the line would be infinite. And if the range is mentioned then line would be finite.
What if all the coordinates are constants or given?
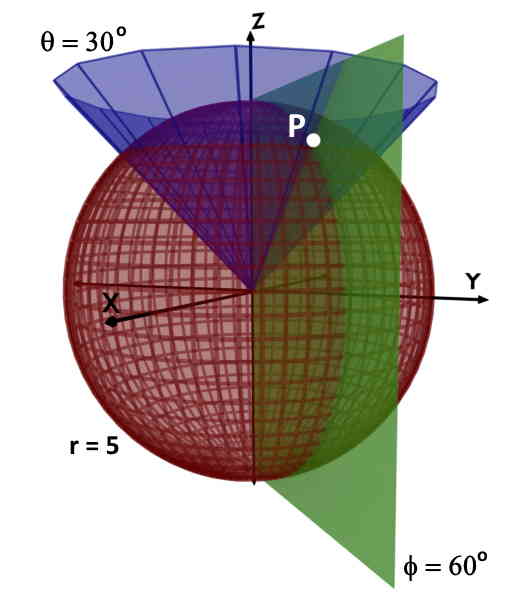
Assume that a point in space is P (5, 600, 300). i.e. r=5; φ=600 and θ=300.
In simple words, this point P is sitting on a sphere having radius 5. And, it is present on the plane, called as vertical half plane making an angle of 600 with the +X axis. In addition, it on curved conical surface making angle 300 with +Z axis.
And the common intersection of all these planes, is our point P, uniquely located in the space.
Conversion of a Point between Spherical and Cartesian Coordinates
We know that, any point or vector in space can be represented using different coordinate systems viz. Cartesian, Cylindrical and Spherical . But keep in mind that we are representing the same point/ vector using different conventions.
We use the coordinate system according to need of our EMT problem. So, there are many instances in Electromagnetics, when you need to convert from one coordinate system to other or vice-versa.
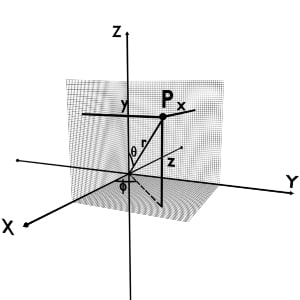
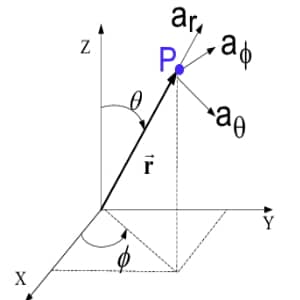
Let us say we are given the point P in space. Now in Cartesian coordinate system coordinates of point P are (x, y, z). x is the perpendicular distance from YZ plane, y is the perpendicular distance from XZ plane and z is the perpendicular distance from XY plane.
At the same time, given point P can also be represented using Spherical coordinate system with coordinates P(r, φ, θ). r is the distance of point from origin, φ is the angle made by vertical half plane with +X-axis and θ is the angle made by the r with +Z-axis.
And now let us draw coordinates for both of these in a single diagram.
From Cartesian to Spherical Coordinate System
Let us assume that we are given with point P in Cartesian Coordinates and we wish to represent the same point in Spherical Coordinates. In simple words, we know the x, y and z for point P and we want r, theta and phi from its x, y and z coordinates.
Getting r coordinate from x, y and z

As ∆ABC is a right angle triangle so applying the Pythagoras theorem to ∆ABC we can directly find the r coordinate. Side AB=r and side BC=z.
But we don’t know the side AC so again apply Pythagoras theorem for right angled ∆ACD. By projecting x and y parallelly we get side AD=x and CD=y.
\therefore AC=\sqrt{x^2\;+\;y^2}
Now apply Pythagoras theorem in ∆ABC; we get
r\;=\;\sqrt{\left(\sqrt{x^2\;+\;y^2}\right)^2+\;z^2}
\therefore r\;=\;\sqrt{x^2\;+\;y^2\;+\;z^2}
Getting θ coordinate from x, y and z
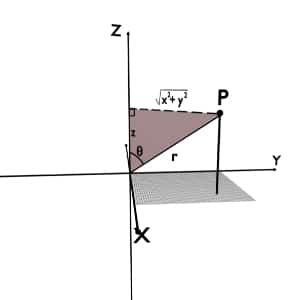
From figure we can directly write,
\cos\left(\theta\right)\;=\;\frac zr
\therefore \theta\;=\;\cos^{-1}\left(\frac zr\right)\;=\;\cos^{-1}\left(\frac z{\sqrt{x^2\;+\;y^2\;+\;z^2}}\right)
\tan\left(\theta\right)\;=\;\frac{\sqrt{x^2\;+\;y^2}}z
\therefore \theta\;=\;\tan^{-1}\left(\frac{\sqrt{x^2\;+\;y^2}}z\right)
For calculating θ, if we use formula of tanθ then answer might be wrong in case of negative z coordinate. If the value of θ we get is negative, then we have to do one more step that is, we have to add 1800 in the final answer.
So for calculating correct value of θ always use formula of cosθ.
Getting φ coordinate from x, y and z
φ in Spherical coordinate system is same as in cylindrical coordinate system.
\phi\;=\;\tan^{-1}\left(\frac yx\right)
We do changes in above formula as per XY quadrant of the point as we have seen in the Cylindrical Coordinate System’s article.
From Spherical Coordinate System to Cartesian
Let us assume that we are given with point P in Spherical Coordinates and we wish to represent the same point in Cartesian Coordinates. In simple words, we know the r, theta and phi for point P and we want x, y and z from its r, theta and phi coordinates.
Getting z from r, θ and φ
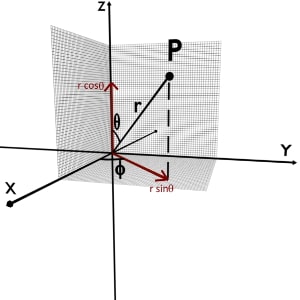
r is making an angle θ with +Z axis. Decompose r into two components i.e. rcosθ along Z axis and rsinθ perpendicular to Z axis in XY plane.
From figure it is clear that, rcosθ is the perpendicular distance of given point from XY plane i.e. distance along Z-axis. So according to the definition of z-coordinate it is nothing but a z-coordinate.
∴ z\;=\;r\;\cos\left(\theta\right)
Getting x and y from r, θ and φ

From figure we can see that, rsinθ is in XY plane making an angle φ with +X axis. Now decompose rsinθ into two components i.e. rsinθcosφ along X axis and rsinθsinφ along Y axis.
rsinθcosφ is the perpendicular distance of given point from YZ plane i.e. distance along X-axis. And rsinθsinφ is the distance of given point from XZ plane i. (sapns2.com) e. along Y-axis.
∴ x\;=\;r\;\sin\left(\theta\right)\;\cos\left(\phi\right)
∴ y\;=\;r\;\sin\left(\theta\right)\;\sin\left(\phi\right)
Example: Represent P(-2, 6, 3) into Spherical
Given point P(-2 ,6, 3) is represented in Cartesian Coordinate System. And we have to asked to represent it in Spherical.
In Cartesian, any point is represented as (x, y, z). Hence, for point P, x=-2; y=6; z=3.
Hence, r\;=\sqrt{x^2\;+\;y^2\;+\;z^2}\;=\;\sqrt{\left(-2\right)^2+6^2+3^2}\;=\;\sqrt{49}\;=\;7
And \theta\;=\cos^{-1}\left(\frac zr\right)\;=\;\cos^{-1}\left(\frac37\right)\;=\;64.62^\circ
As x-coordinate is negative and y-coordinate is positive, it lies in second quadrant, we have,
\phi\;=\;180^\circ\;-\;\tan^{-1}\left|\frac yx\right|\;=\;180^\circ-\tan^{-1}\left|\frac6{-2}\right|\;=\;108.44^\circ
Hence P(-2, 6, 3) ≡ P(7, 108.440, 64.620)
How are the vectors represented in the Spherical Coordinate System?
The general way of representation for the vectors is as follows:
\overrightarrow A=A_r\overrightarrow{a_r}\;+\;A_\phi\overrightarrow{a_\phi}\;+\;A_\theta\overrightarrow{a_\theta}
Ar , Aφ and Aθ are the r, Phi and Theta components of the vector while ar , aφ and aθ are the unit vectors of Spherical Coordinate System.
How are the Unit Vectors defined for a Spherical Coordinate System?
Any vector in a Spherical coordinate system is represented using mutually perpendicular unit vectors.
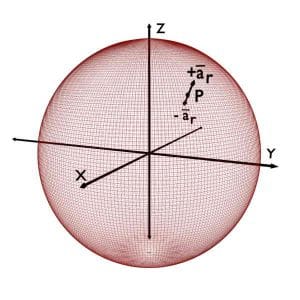
Unit vector \overrightarrow{a_r} at the given point P, is a vector of unit magnitude; perpendicular to r = constant plane and pointing in the increasing r direction.
While, -{\overrightarrow a}_r is a vector of unit magnitude; perpendicular to r = constant plane and pointing in the decreasing r direction.
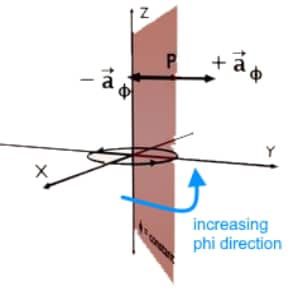
Unit vector \overrightarrow{a_\phi} at the given point P, is a vector of unit magnitude; perpendicular to phi (φ) = constant plane and pointing in the increasing phi direction i.e. anticlockwise.
Unit vector -{\overrightarrow a}_\phi is a vector of unit magnitude; perpendicular to phi (φ) = constant plane and pointing in the decreasing phi direction i.e. clockwise.
It is same as in Cylindrical coordinate system.
Unit vector \overrightarrow{a_\theta} at the given point P, is a vector of unit magnitude; perpendicular to theta (θ) = constant plane and pointing in the increasing theta direction.
Unit vector -{\overrightarrow a}_\theta is a vector of unit magnitude; perpendicular to theta (θ) = constant plane and pointing in the decreasing theta direction.
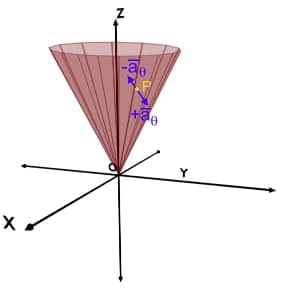
So, any vector in Spherical coordinate system, is a combination or vector addition of r component, phi component and theta component presented by unit vectors \pm{\overrightarrow a}_r \pm{\overrightarrow a}_\theta and \pm{\overrightarrow a}_\phi respectively.
Conversion of a Vector between Spherical and Cartesian
For Cartesian Coordinate System, the general way of representation for the vectors is as follows:
\overrightarrow A\;=\;A_x\overrightarrow{a_x}\;+\;\;A_y\overrightarrow{a_y}\;+\;\;A_z\overrightarrow{a_z}
Ax, Ay and Az are the X, Y and Z components of the vector while ax, ay and az are the unit vectors of Cartesian Coordinates.
For Spherical Coordinate System, the general way of representation for the vectors is as follows:
\overrightarrow A\;=\;A_r\overrightarrow{a_r}\;+\;\;A_\theta\overrightarrow{a_\theta}\;+\;\;A_\phi\overrightarrow{a_\phi}
Ar, Aθ and Aφ are the r, θ and φ components of the vector while ar, aθ and aφ are the unit vectors of Spherical Coordinates.
Let us find the expression for cartesian unit vectors in terms of spherical unit vectors.
Relation between Cartesian and Spherical Unit Vectors
ar, aθ and aφ are three mutually perpendicular unit vectors of spherical coordinate system of any point P and now we have to find their total equivalent along +X-axis, +Y-axis and +Z-axis to get the expression for unit vector ax, ay and az.
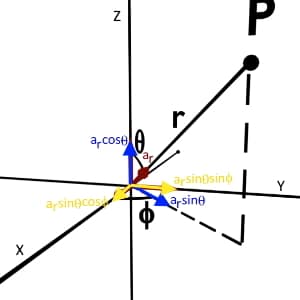
Consider unit vector ar. Let us find its component along X, Y and Z axis.
Firstly, decompose ar into two components i.e. ar cosθ along Z-axis and ar sinθ in XY plane.
Now again decompose ar sinθ into ar sinθcosφ along X-axis and ar sinθsinφ along Y-axis.
All the three components of unit vector ar is shown in the figure.
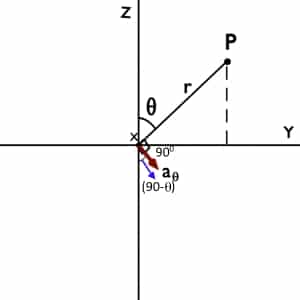
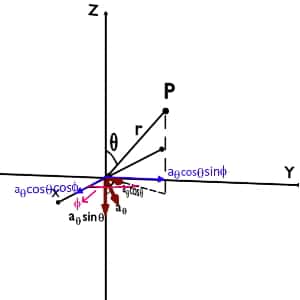
Let us consider unit vector aθ.
We know that aθ is perpendicular or normal to θ equal to constant plane. From following figure we can say that unit vector aθ is making an angle of (90-θ) with negative Z axis.
Now we can decompose aθ in two components i.e. aθ cos(90-θ) = aθ sinθ along negative Z-axis. And aθ sin(90-θ) = aθ cosθ in XY plane.
aθ cosθ is making an angle φ with +X-axis. Again aθ cosθ can decompose into two components that is aθ cosθcosφ along X-axis and aθ cosθsinφ along Y-axis.
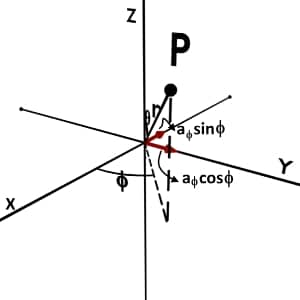
Now consider unit vector aφ.
It is same as we see in Cylindrical to Cartesian conversion.
The components aφsinφ is along negative X axis and aφcosφ along positive Y axis.
Now let us collect all the components of unit vectors ar, aθ and aφ in single diagram so we can easily find the resultant X, Y and Z components of all these unit vectors. In other words, from the diagram below, we can easily find the expression for cartesian unit vectors ax, ay and az in terms of spherical unit vectors ar, aθ and aφ.
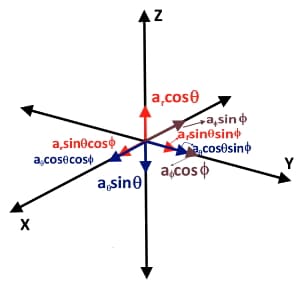
So we directly write the expressions as,
a_x\;=\;a_x\;\sin\theta\;\cos\phi\;+\;a_{\theta\;}\cos\theta\;\cos\phi\;-\;a_\phi\sin\phi
a_y\;=\;a_y\;\sin\theta\;\sin\phi\;+\;a_{\theta\;}\cos\theta\;\sin\phi\;+\;a_\phi\cos\phi
a_z\;=\;a_r\;\cos\theta\;-\;a_{\theta\;}\sin\theta
Relation between Cartesian and Spherical Vectors
Let us say we are given with vector \overrightarrow A=\;A_x\overrightarrow{a_x\;}+A_y\overrightarrow{a_y\;}+A_z\overrightarrow{a_z\;} which is represented with Cartesian Coordinate system and we wish to represent the same vector with Spherical Coordinate system.
Now, we have the relation between Cartesian and Spherical unit vectors so substitute the values of ax, ay and az .
\overrightarrow A=A_x(a_r\sin\theta\cos\phi+a_\theta\cos\theta\cos\phi-a_\phi\sin\phi)\;+\;A_y(a_r\sin\theta\sin\phi+a_\theta\cos\theta\sin\phi+a_\phi\cos\phi)\;+\;A_z(a_r\cos\theta-a_\theta\sin\theta)
Arranging the terms, we get
\overrightarrow A=(A_x\sin\theta\cos\phi+A_y\sin\theta\sin\phi+A_z\cos\theta)\overrightarrow{a_r}\;+\;(A_x\cos\theta\cos\phi+A_y\cos\theta\sin\phi-A_z\sin\theta)\overrightarrow{a_\theta}\;+\;(-A_x\sin\phi+A_y\cos\phi)\overrightarrow{a_\phi}
But in Spherical Coordinate system, general form of vector is given as,
\overrightarrow A\;=\;A_r\overrightarrow{a_r}\;+\;A_\theta\overrightarrow{a_\theta}\;+\;A_\phi\overrightarrow{a_\phi}
Now comparing above equations, we get,
A_r\;=\;A_x\;\sin\theta\cos\phi\;+A_y\;\sin\theta\sin\phi\;+\;A_z\;\cos\theta\;
A_\theta\;=\;A_x\;cos\theta\cos\phi\;+A_y\;\cos\theta\sin\phi\;-\;A_z\;\sin\theta\;
A_\phi\;=\;-A_x\;\sin\phi\;+A_y\;\cos\phi\;
This can be easily memorized in the matrix form as:
\begin{bmatrix}A_r\\A_\theta\\A_\phi\end{bmatrix}\;=\;\begin{bmatrix}\sin\theta\cos\phi&\sin\theta\sin\phi&\cos\theta\\\cos\theta\cos\phi&\cos\theta\sin\phi&-\sin\theta\\-\sin\phi&\cos\phi&0\end{bmatrix}\begin{bmatrix}A_x\\A_y\\A_z\end{bmatrix}
This transformation matrix can be used to obtain components of a vector in spherical coordinates if we already have the components of that vector in cartesian. In simple words, it is used to convert given vector in Cartesian to Spherical.
Now, had the vector represented in Spherical and we needed to convert it into Cartesian. That means, we already have r, theta and phi components of the vector; but we need x, y and z components. So working in a similar manner, we would get transpose of the above matrix.
Hence, the transformation of the vector from one to other is given as,
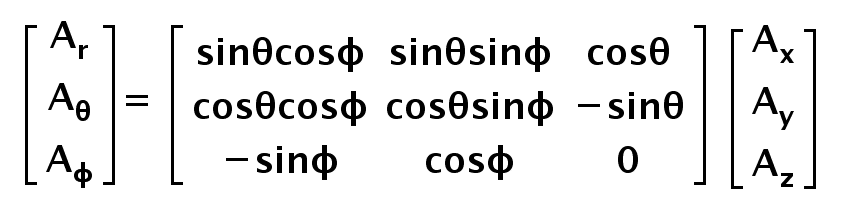

Example : Represent A=yax+(x+z)ay into Spherical Coordinate System.
Given vector is in Cartesian so comparing with A\;=\;A_x\;\overrightarrow{a_x}\;+\;A_{y\;}\overrightarrow{a_y\;}\;+\;A_z\;\overrightarrow{a_z}
We get, A_x\;=\;y;\;A_{y\;}=\;(x+z);\;A_z\;=\;0
Now we want Spherical Coordinates,
\begin{bmatrix}A_r\\A_\theta\\A_\phi\end{bmatrix}\;=\;\begin{bmatrix}\sin\theta\cos\phi&\sin\theta\sin\phi&\cos\theta\\\cos\theta\cos\phi&\cos\theta\sin\phi&-\sin\theta\\-\sin\phi&\cos\phi&0\end{bmatrix}\begin{bmatrix}A_x\\A_y\\A_z\end{bmatrix}
\begin{bmatrix}A_r\\A_\theta\\A_\phi\end{bmatrix}\;=\;\begin{bmatrix}\sin\theta\cos\phi&\sin\theta\sin\phi&\cos\theta\\\cos\theta\cos\phi&\cos\theta\sin\phi&-\sin\theta\\-\sin\phi&\cos\phi&0\end{bmatrix}\begin{bmatrix}y\\(x+z)\\0\end{bmatrix}
A_r\;=\;y\;\sin\theta\cos\phi\;+\;(x+z)\;\sin\theta\sin\phi
A_\theta\;=\;y\;\cos\theta\cos\phi\;+\;(x+z)\;\cos\theta\sin\phi
A_\phi\;=\;-y\;\sin\phi\;+\;(x+z)\;\cos\phi
In Spherical Coordinates,
\overrightarrow A\;=\;A_r\;\overrightarrow{a_r}\;+\;A_\theta\;\overrightarrow{a_\theta}\;+\;A_\phi\;\overrightarrow{a_\phi}
\overrightarrow A\;=\;\lbrack y\sin\theta\cos\phi+(x+z)\sin\theta\sin\phi\rbrack\overrightarrow{a_r} +\lbrack y\cos\theta\cos\phi+(x+z)\cos\theta\sin\phi\rbrack\overrightarrow{a_\theta} +\lbrack-y\sin\phi+(x+z)\cos\phi\rbrack\overrightarrow{a_\phi}
In the last step we still have the Cartesian Coordinate variables. So, convert these x, y, z variables into equivalent Spherical r, θ, φ variables.
We know that,
x\;=\;r\;\sin\theta\cos\phi; y\;=\;r\;\sin\theta\sin\phi; z\;=\;r\;\cos\theta
Substitute all the variables in eqn(1) and after simplification we get,
\overrightarrow A=r\lbrack\sin^2\theta\cos\phi\sin\phi+(\sin\theta\cos\phi+\cos\theta)\sin\theta\sin\phi\rbrack\overrightarrow{a_r}
+\;r\left[\sin\theta\sin\phi\cos\theta\cos\phi+(\sin\theta\cos\phi+\cos\theta)\cos\theta\sin\phi\right]\overrightarrow{a_\theta}
+r\lbrack-\sin\theta\sin^2\phi+(\sin\theta\cos\phi+\cos\theta)\cos\phi\rbrack\overrightarrow{a_\phi}
If specific point is given then we can find \sin\theta,\;\sin\phi,\;\cos\theta,\;\cos\phi to get the specific vector at that point.
Cylindrical to Spherical conversion or vice-versa
For doing the Cylindrical to Spherical conversion, firstly convert Cylindrical to Cartesian conversion and secondly Cartesian to Spherical conversion.
Similarly, for Spherical to Cylindrical, firstly convert Spherical to Cartesian and then Cartesian to Spherical. It is always easier to convert using two steps rather than remembering more formulas.
Hope you enjoyed the article. Amplify your concepts by sharing with others.