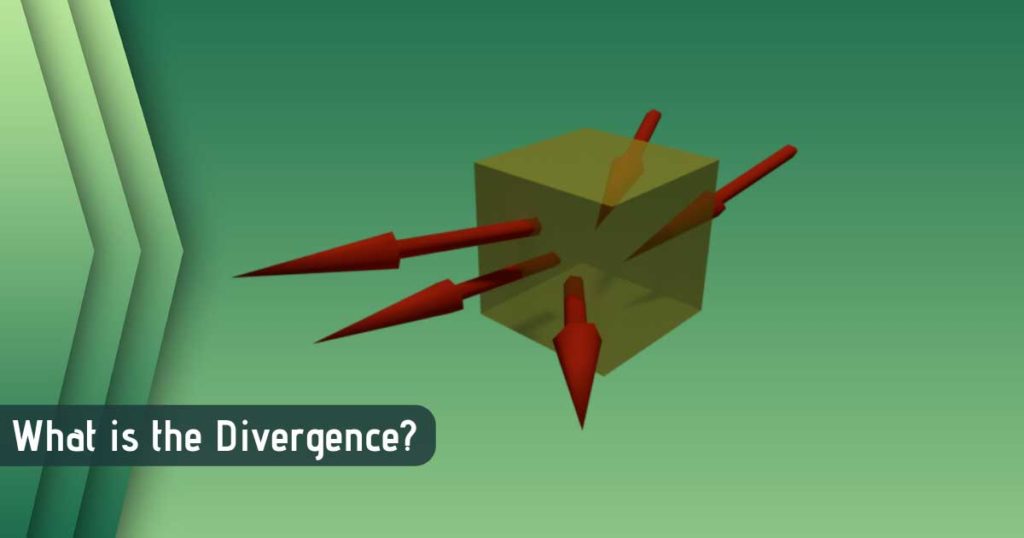
The Divergence of a vector field is a measure of the net flow of the flux around a given point. It is a basic term and used in many terminologies of Electromagnetics. This article defines the divergence of a vector field in detail.
A formal definition of Divergence
The divergence of vector field at a given point is the net outward flux per unit volume as the volume shrinks (tends to) zero at that point.
Its meaning in simple words
Consider any vector field and any point inside it. Let us assume an infinitesimally small hypothetical volume around the considered point.
If the lines of the field that are going outside the hypothetical volume are more than that of coming inside it then we can say that the vector field is spreading outwards around that point. Technically, the field is diverging around that point.

The simplest synonym for the divergence is “outgoingness”. More is the divergence more are the field lines coming outside around that point and it should be considered as positive divergence. In contrast to that, if field lines tend to come inside then we can say the field is accumulating at that point which is opposite to “outgoingness” and hence considered as a negative divergence.
The divergence explained in detail
In simple words, it would tell us about the nature of the field at the given point. By the word nature I mean to say whether it is diverging or conversing(negative divergence). It should also indicate the extent of divergence for analyzing two or more points.
Consider again the vector field and let us say we are interested in finding the divergence at point P as shown in the figure above. Consider the infinitesimally small close surface preferably a cube around the point P having volume ∆v.
The simplest synonym for the divergence is “outgoingness”. More is the divergence more are the field lines coming outside around that point and it should be considered as positive divergence. In contrast to that, if field lines tend to come inside then we can say the field is accumulating at that point which is opposite to “outgoingness” and hence considered as a negative divergence.
What is the Close Surface
The close surface is the outer surface of some actual 3D object. Open surface or normal surface if it posses the only area. Now we know that the actual 3D object will have the volume and outer surface area.

We are intentionally assuming the closed surface around the point so that we could find the flux of the field that is coming out of this close surface. Can you guess why would we calculate the flux of the field coming out of this surface?
The reason is quite simple! We can infer about the outgoingness of the field by counting the total number of field lines that are coming outside this close surface versus the total number of lines that are coming inside of it. And the best way to predict the lines of the field is the flux.
Now how to find the net flux coming out of this cube? Simple, using surface integration. We have to apply the surface integration for each surface (considering the direction of unit vector outward) of the cube and every time the answer will be the total flux coming out of that respective surface. Combining all, the total close surface integration will give us the net flux that is coming out of the cube/close surface.

Now, if the answer to this net flux is positive then we can say a few lines of the field are coming outside more than that are coming inside. Hence the field is diverging.
If the net flux is negative then we can say that there are more lines coming into the cube than leaving hence converging.
Finally, if the net flux is zero then we can say the lines which are entering into the cube are leaving from it. Hence the zero divergence.
So all the necessary properties that define the divergence can be extracted from this net flux coming out of the infinitesimal (very small) close surface around the given point. Precisely we should keep this close surface as small as possible. In other words, its volume should be approaching zero. Hence finally the divergence can be defined and represented as below.
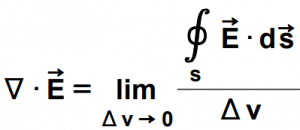
The Divergence Symbol
The divergence operation is applied to the vector function/field. Let us say the vector field is denoted as A then the divergence symbol or the representation is as follows-

The Divergence Formulas in different coordinate systems
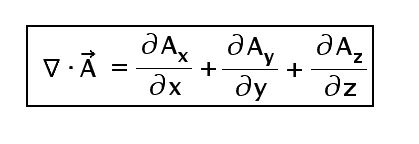
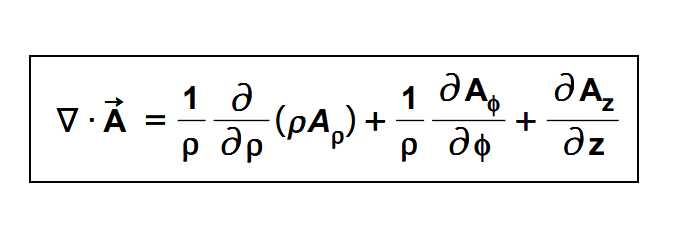
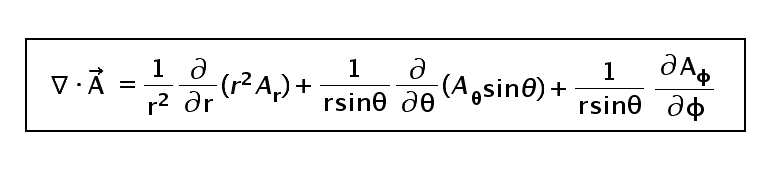
Intuitive derivation of the Divergence formula
The divergence indicates the outgoingness of the field at the point of interest. Let vector field A is present and within this field say point P is present. The vector field means I want to say the given vector function of x, y and z. I am assuming the Cartesian Coordinates for simplicity. So the field is A(x,y,z). Let us say we want to analyze the divergence of the field around this point P.
The divergence can be thought as the net number of lines or net flux of the field coming out of the infinitesimal volume supposed at the given point. Isn’t it? So let us assume the very small or infinitesimal volume in the form of the cube around the point P.
As we know from the knowledge of the Cartesian Coordinate System that volume can be formed by varying all three lengths i.e. along X, Y and Z axes. So let us say our infinitesimal volume have the edges dx, dy and dz. In other words, it would have the volume dv = dx dy dz. Point P is in the heart of the cube.
The vector field A is present everywhere and hence at P also. Let the coordinates of point P are (a,b,c) and value of the function/field at this point P (a,b,c) is A(a,b,c).
Now, you might be knowing about the Taylor Series. It is a mathematical expansion series of the function around the specific point. In other words, by using Taylor Series expansion, we actually look at the function from the perspective of the given point. We express the given function using the value of the function at that specific point and variation of the function (of course using derivatives) around that point. Actually, the reason behind this discussion is we are going to express our vector field/function using Taylor Series at point P.
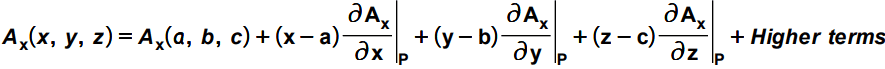
For simplicity consider only x component of the field. Let us leave the y and z components, which can be easily be written by analogy. So with the use of Taylor Series expansion, the x component of the given function A can be expressed as below. Note that we are just representing the given function with another way. This wouldn’t change anything of the original function. We are doing so for our ease of calculations.
On the similar lines the Ay and Az components can be expressed for the given function A. We can also neglect the higher order derivative term as we are considering a very small volume. So we have just represented our given vector field by different presentation i.e. by using the series. With this representation, you can see that the function is reframed as its value at point P(a,b,c) and change of the function along X, Y and Z-axis from that point.
Now let us recall that the divergence is nothing but the net flux of the vector field that is coming out from the small volume (close surface) formed around P. Now how do we calculate the flux of the field? Recall the surface integration. We find the flux using the following formula. Here A is the vector field and ds is the infinitesimal surface of the given surface from which the flux is to be calculated.
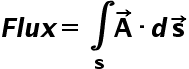
Now for our case, we can neglect the integration as we are already assuming the infinitesimal case. So in simple words for our case flux would be the multiplication of the vector field and infinitesimal area.
Now as seen from the figure, if I want to calculate the total flux that is coming out of this cube then I have to apply the flux formula for six times. Each time for a single surface, isn’t it? But for simplicity, we have considered only the x-component of the given field. So as you can see from the figure, we will calculate the flux only for the left and right surfaces. The x-components of the given field would go tangential to top, bottom and side surfaces. So the flux contribution for these surface would be zero for the Ax.
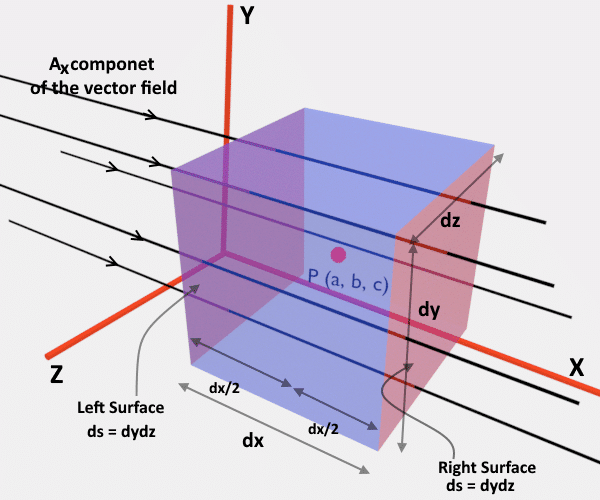
So let us take the right side surface. The area of this surface is dydz. Now for the flux, we want the value of the field at the location of this surface. We will write it using the Taylor Series expansion as seen above. Let me represent here once again.
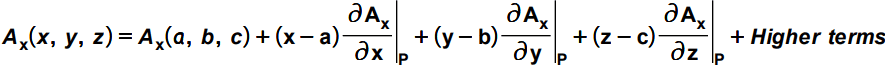
From the above expression, at very first, we can omit the higher derivative terms as we are dealing with the infinitesimal case. Secondly, the derivative terms with respect to y and z can also be neglected, as for the simplicity, we are considering only the x components of the given field i.e. Ax. And the y and z components of the field are not going to contribute to the flux of this surface as they will flow tangentially to it. So the above formula can be narrowed down to this-
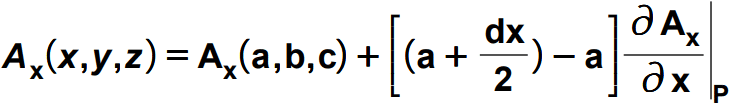
Note here the value of the x at the position of the surface is a+(dx/2) as seen from the figure. So,
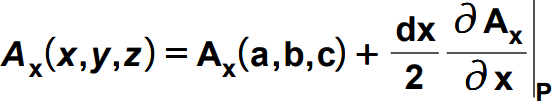
So the flux through this right surface is given as follows by multiplying the Ax with the area of the surface.
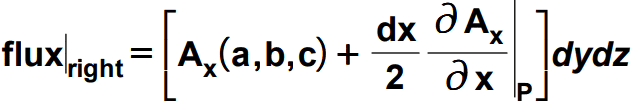
Now for the left side surface, a value of the x is a–(dx/2). Also, the ds value would be (-dydz) for taking the account of the direction of the area vector always out of the volume and hence pointing to the negative X-direction. So putting on the same expression above, we will get the flux for this left side surface as shown below.
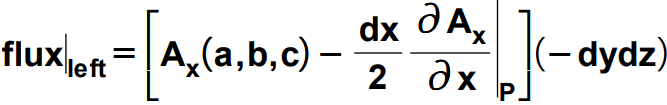
So the net flux through these left and right surfaces is obtained by adding both of the above expressions which would lead to as shown below.
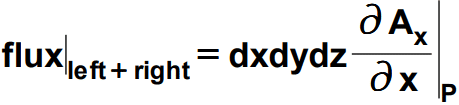
The y component of the field i.e. Ay comprises the flux linked to the top and bottom surfaces. While the z component Az make up the flux through the front and back ones. So working on the similar lines flux through these surfaces can be written as follows:
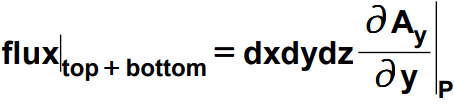
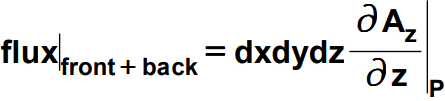
So considering all the surfaces i.e. the net flux coming out of this infinitesimal volume is given as:-
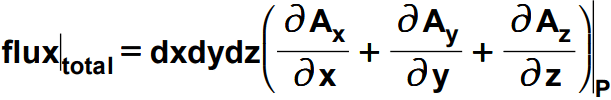
Now again recall the definition of the divergence. Let me state it once again in simple words, it is the total flux per unit volume. Right? Check the above expression, the term dxdydz is nothing but the infinitesimal volume, dv that we have considered around the given point. So if we divide by the dv i.e. dxdydz both sides of the above equation, boom! we get our expression of the divergence as follows:-
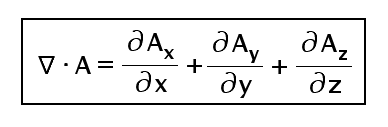
The same expression can be modified for the cylindrical and spherical coordinates by converting the variables from cartesian to respective coordinates and obtained as stated above.
The Divergence properties that you must know
Divergence operates on the Vector and gives the Scalar
As we have seen from the definition, the easiest way to understand the Divergence meaning is the “outgoingness” of the vector field at a given point. Isn’t it? That means the divergence operation operates on the vector field/function and gives back the number i.e. scalar indicating the measure of the “outgoingness”. Greater is the number greater the field is diverging.
The sign of the Divergence depicts the nature of the field
Divergence, as the name suggests, is an outgoingness. The positive sign indicates that the field has certain divergence at that point in the outward direction. In other words, field lines are spreading away around that point.
But if the sign of the divergence is negative then the field lines are not spreading but converging around that point. This means the field is converging at that point.
Zero Divergence depicts the uniform field
If the answer of the Divergence is zero then we can conclude that the field lines are neither spreading nor contracting. In other words, the number of lines entering per unit infinitesimal volume that is assumed around the given point is equal to the number of lines leaving it. So the field can be considered uniform around the zero divergence point.

The Divergence operation on Scalar field makes no sense
Always remember the divergence operation is defined for the vector fields. It gives us an idea about the nature of the field around the given point. Hence the divergence of a scalar field makes no sense.
The Divergence Theorem
It states that the total outward flux of vector field say A, through the closed surface, say S, is same as the volume integration of the divergence of A.
Consider the vector field A is present and within the field, say, a closed surface preferably a cube is present as shown below at point P.
Now, what is the closed surface? It is the surface of any 3-d body. In other words, the close surface encloses the volume inside it. Hence along with the surface area, it also possesses the volume. In our illustration, we have considered the cube which has six surfaces enclosing the volume.

So we need to find the flux coming out of each of these six surface in order to calculate the net outward flux coming out of the closed surface i.e. cube. Isn’t it?
Now you also know that we calculate the flux of the vector field for the given surface using the surface integration. Correct? So the net flux through this cube or closed surface would be the addition of surface integrations of all the six surfaces. This can be represented as shown below. You can see a small circle at the center of the integration sign. This indicates that this term is the addition of all the individual integrals of each surface or the net flux that is coming out of this closed surface (cube).

Now, according to the Divergence Theorem, the net flux of the field that is coming out of the closed surface is equal to volume integration of the divergence of that vector field. The volume for the integration must be obviously the volume that is enclosed by the given closed surface. In our case, the volume enclosed by the cube.
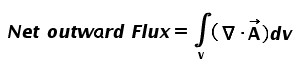
So we can easily equate the above equations and lead to as shown below.
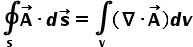
In simple words, we can say that the theorem relates the surface integration with the volume integration. But most important! The surface on which we are applying the theorem must be closed surface. Otherwise, it wouldn’t be possible to apply it. It is very simple. If it is not the closed surface then we won’t get the volume inside. Hence no volume integration.
So the Divergence Theorem can be used only for the closed surfaces.
Thus the flux of the field can be calculated using surface integration in any case (open or closed surface). In addition, it can also be found out by volume integration in case of the closed surfaces.
Do not forget to check our Awesome GATE courses.